Question

Алгебра срочно, пожалуйста. 3 и 4.
С графиком/ рисунком.​

Answer 1

Ответ:

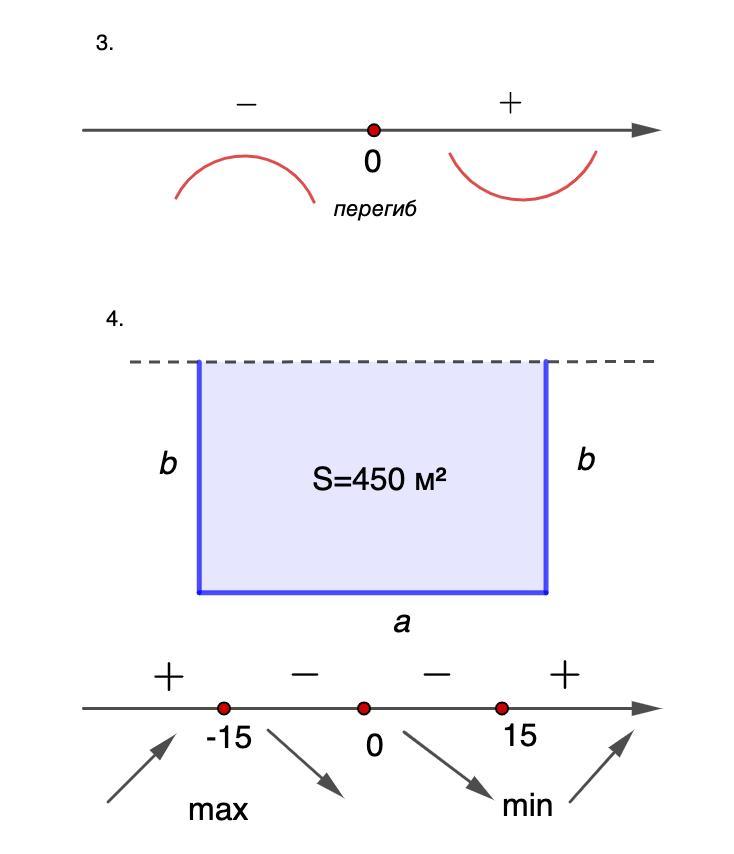
3. Функция выпукла вниз на промежутке [0; +∞);

функция выпукла вверх на промежутке (-∞; 0]

х перегиба = 0.

4. Наименьшая длина забора равна 60 м.

Объяснение:

3. Для функции y = x³ - 5x + 2 найдите промежутки выпуклости вверх. выпуклости вниз и координаты точки перегиба её графика.

4. Участок прямоугольной формы площадью 450 м² огорожен забором с трех сторон. Найдите наименьшую длину забора.

3.  y = x³ - 5x + 2

Сначала найдем производную первого порядка.

y' = 3x² - 5

Затем найдем производную второго порядка, приравняем к нулю и найдем корни.  

y'' = 3 · 2x = 6x

y'' = 0   ⇒ 6x = 0   или х = 0

Отметим корень на числовой оси и определим знаки второй производной на промежутках.  

См. вложение.

• Если производная второго порядка положительна, то функция вогнута (выпукла вниз), если отрицательна - выпукла вверх.

Функция выпукла вниз на промежутке [0; +∞);

функция выпукла вверх на промежутке (-∞; 0]

• Точка, в которой вторая производная меняет знак, называется точкой перегиба.

⇒ х перегиба = 0.

4. S = 450 м²

• Площадь прямоугольника равна произведению смежных сторон.

                         S = ab,

• где а и b - стороны прямоугольника.

ab = 450   ⇒  a = 450/b

Так как участок огорожен с трех сторон, то длина забора будет равна

C = a + 2b

или

$\displaystyle\bf C=\frac{450}{b} +2b=\frac{450+2b^2}{b}$

Получили функцию С(b).

Найдем ее минимальное значение.

Найдем производную, приравняем к нулю и найдем корни.

$\displaystyle\bf C'=\frac{4b\cdot b-(450+2b^2)\cdot 1}{b^2} =\frac{2b^2-450}{b^2}$

$\displaystyle\bf C'=0\;\;\;\Rightarrow \;\;\;\frac{2b^2-450}{b^2}=0\\\\2(b^2-225)=0;\;\;\;b\neq 0\\\\b=\pm15$

Отметим их на числовой оси и определим знаки производной на промежутках. Не забываем про точку b = 0, в которой производная не существует.

См. вложение.

• Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке  - минимум.

⇒ минимальное значение функция имеет в точке b min = 15.

Получили b = 15м, тогда а = 450/15 = 30 (м).

Наименьшая длина забора равна:

С = 15 · 2 + 30 = 60 (м)