Предмет: Геометрия,
автор: Vanyok4
У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки 5 см і 12 см. Знайдіть радіус кола, якщо периметр трикутника дорівнює 60 см.
Ответы
Автор ответа:
0
Ответ:
3 см.
Объяснение:
Дано: ΔАВС, ∠С=90°; т. ОН=ОК=ОЕ=радіус вписаного кола (r); Р(АВС)=60 см.; АН=12 см, ВН=5 см. r - ?
Відрізки дотичних, проведених до кола з однієї точки, рівні між собою.
АК=АН=12 см, ВЕ=ВН=5 см.
ОК=ОН=ОЕ=СЕ=х см, тоді за теормою Піфагора
АВ²=АС²+ВС²; 17²=(12+х)²+(5+х)²; 289=144+24х+х²+25+10х+х²;
х²+17х-120=0; за теоремою Вієта х=-20 (не підходить) х=3.
r=3 cм.
Приложения:
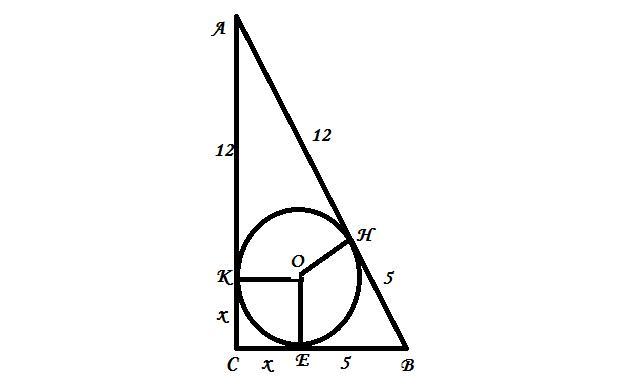
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Биология,
автор: surkovartem72
Предмет: Қазақ тiлi,
автор: merisaaauai
Предмет: Математика,
автор: katekstkani