Алгебра, срочно!1 и 2 с графиками.
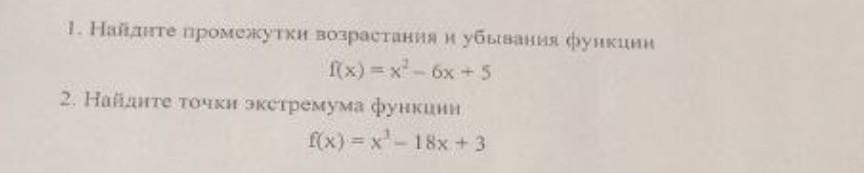
Ответы
Ответ:
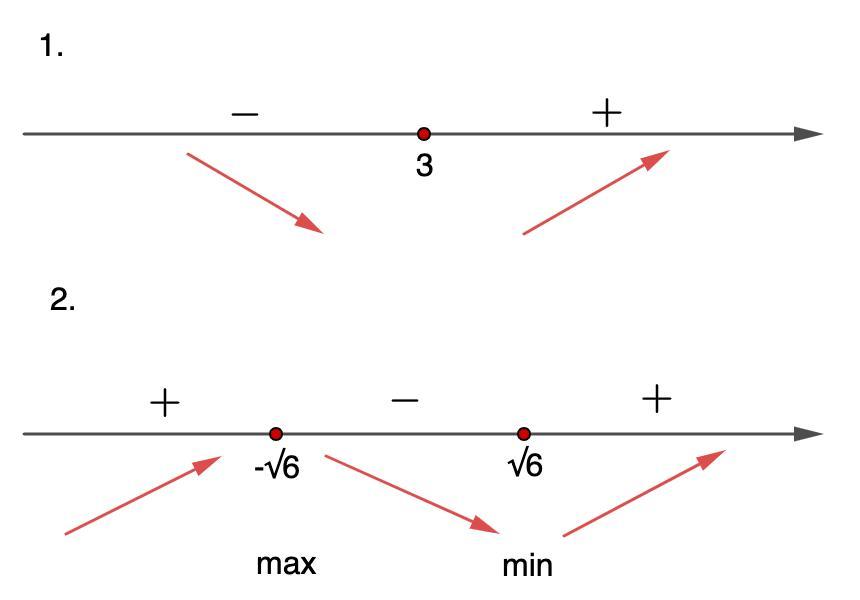
1. Функция возрастает на промежутке [3; +∞).
Функция убывает на промежутке (-∞; 3]
2. x max = -√6; x min = √6.
Объяснение:
1. Найти промежутки возрастания и убывания функции:
f(x) = x² - 6x + 5
Найдем производную, приравняем к нулю и найдем корни.
f'(x) = 2x - 6
f'(x) = 0 ⇒ 2x - 6 = 0
x = 3
Отметим их на числовой оси и определим знаки производной на промежутках.
Если, например, х = 0, то f'(x) = -6 < 0 ⇒ знак Минус.
Если, например, х = 4, то f'(x) = 2 > 0 ⇒ знак Плюс.
- Если "+" - функция возрастает, если "-" - функция убывает.
Функция возрастает на промежутке [3; +∞).
Функция убывает на промежутке (-∞; 3]
2. Найти точки экстремума функции:
f(x) = x³ - 18x + 3
Найдем производную, приравняем к нулю и найдем корни.
f'(x) = 3x² - 18 = 3(x - √6)(x + √6)
x₁ = √6; x₂= -√6
Отметим их на числовой оси и определим знаки производной на промежутках.
Если, например, х = 0, то f'(x) = -18 < 0 ⇒ знак Минус.
Если, например, х = -4, то f'(x) = 30 > 0 ⇒ знак Плюс.
Если, например, х = 4, то f'(x) = 30 > 0 ⇒ знак Плюс.
- Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.
⇒ x max = -√6; x min = √6