Предмет: Геометрия,
автор: Uklin22
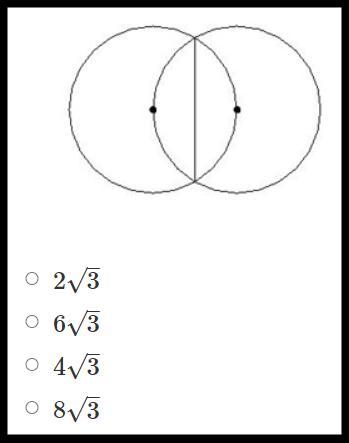
Даны две окружности, расположенные так, что одна окружность проходит через центр другой окружности.
Найдите радиусы данных окружностей, если длина общей хорды равна 6 .
Определите их сумму.
Приложения:
ГАЗ52:
4√3
Ответы
Автор ответа:
1
Ответ: =4√3
Объяснение:
Проведи О1О2 . Для обеих окружностей этот отрезок- радиус.
Значит общая хорда АВ , пересекаясь с О1О2 делится точкой пересечения К пополам . О1О2 также делится точкой К пополам.
Если ОК=х, то радиус =2х,
Тогда О1К=х , ОА=2х, АК=3 . ΔО1АК прямоугольный с гипотенузой О1А. По теореме Пифагора находим х.
О1К²+АК²=О1А² => x²+3²=(2x)² => x²+9=4x²=> 9=3x² => x=√3,
радиус =2х=2√3=> 2 радиусa =4х =4√3,
Похожие вопросы
Предмет: Алгебра,
автор: sazonovevgen76
Предмет: Русский язык,
автор: mazanikvarvara
Предмет: География,
автор: KonfetkaUwU
Предмет: Геометрия,
автор: Radmigo
Предмет: Другие предметы,
автор: ismagilovaviruss