Как это решить?
Помогите, пожалуйста)

Ответы
Ответ:
Площа прямокутного трикутника визначається за формулою:
S = 1/2*AB*BC
До основи прямокутного трикутника проведена медіана. Медіана проведена в прямокутному трикутнику до гіпотенузи дорівнює половині гіпотенузи. Отже, ми можемо знайти сторону АС
АС=4*2 = 8 см
Один із кутів прямокутного трикутника = 30 градусів. Катет, що лежить проти кута 30 градусів в прямокутному трикутнику дорівнює половині гіпотенузи. Отже, АВ = 8:2 = 4 см
За теоремою Піфагора знайдемо катет ВС:
ВС^2 = AC^2 - AB^2
BC^2 = 8*8 - 4*4 = 48
ВС = = 4
см
S =1/2*4*4 = 8
см2
Відповідь: В
Пошаговое объяснение:
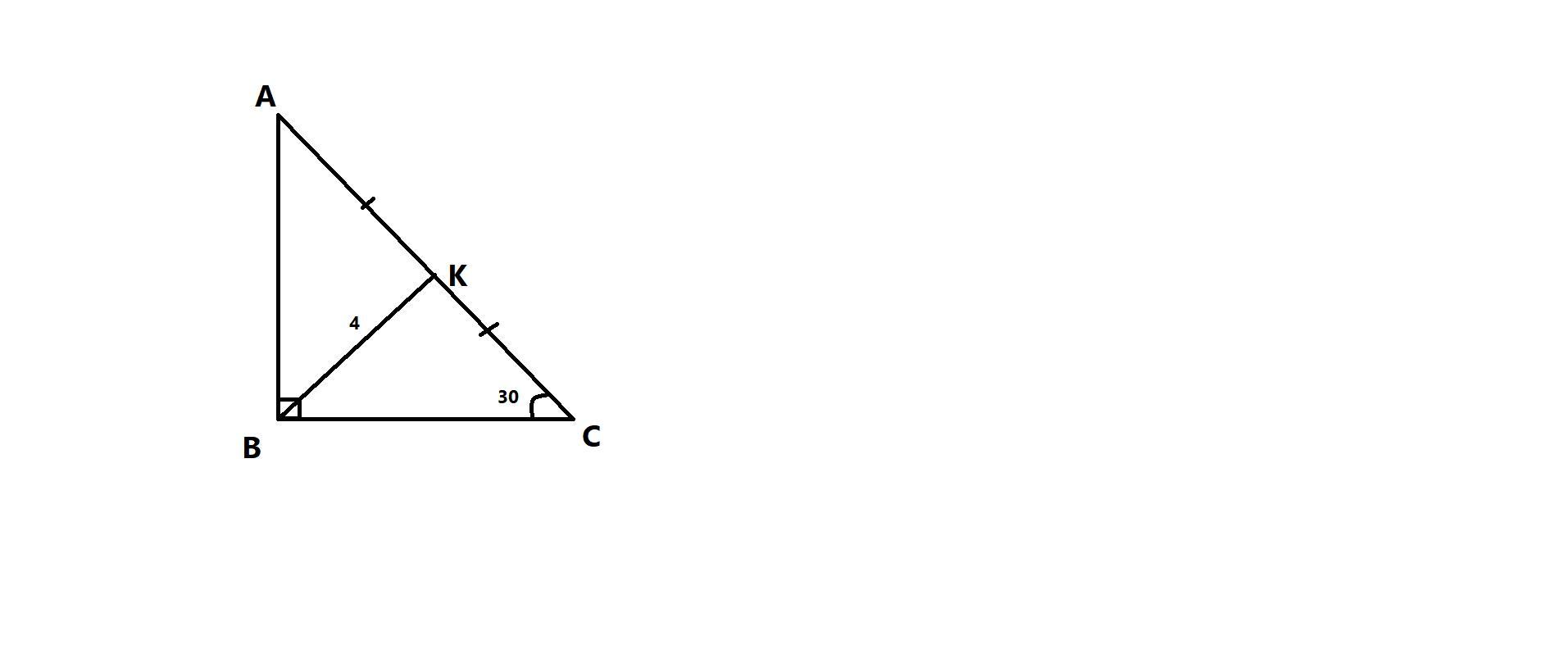
Пускай нам дан △ABC (∠C=90°), ∠A=30°, CM - медиана
По свойству медианы прямоугольного треугольника, проведённой из вершины прямого угла: CM = AM = BM = 4 см
AB = AM + BM = 4 см + 4 см = 8 см
По свойству катета, лежащего напротив угла в 30°: BC = ½AB = ½ * 8 см = 4 см
По т. Пифагора: (см)
Найдём площадь этого прямоугольного треугольника: (см²)
Ответ: B) см²
