Question

Алгебра. Даю 100 балів. потрібно вирішити завдання з максимальним поясненням щоб було усе зрозуміло будь ласка.

з дуже детальним поясненням будь ласка

Answer 1

Ответ:

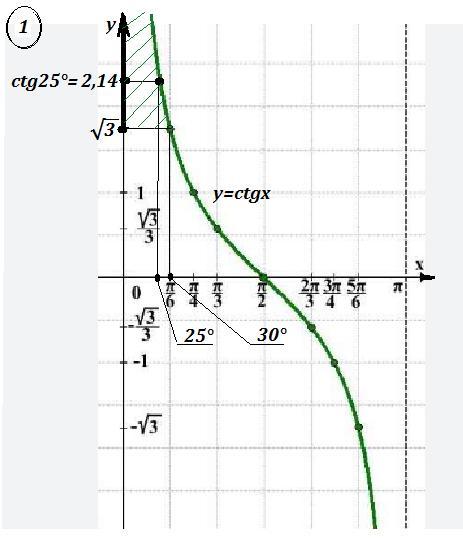
1)  Найти промежуток, которому принадлежит значение  ctg25°  .

Угол в 25°  находится в промежутке между 30°  и  0° , то есть

0°<25°<30° . Это углы 1 четверти . В 1 четверти функция  y=ctgx  убывает. Значит большему значению аргумента соответствует меньшее значение функции , то есть  ctg30°<ctg25°<ctg0°  .

ctg30° = √3  ,  а  ctg0°  не существует, при стремлении аргумента к 0 значение функции y=ctgx  неограниченно возрастает, стремится к +∞  . Поэтому   √3 < ctg25° < +∞  , или   ctg25° ∈ (√3 ; +∞ ) .

Можно в этом убедиться, найдя значение функции по таблицам :

ctg25° ≈ 2,1444  ,  ctg30° = √3 ≈ 1,7321   ⇒     1,7321 < 2,1444  

Ответ:  Д ) .  

2)  Записать в порядке возрастания :   $\bf 2^{15}\ ,\ 4^{10}\ ,\ 10^5$  .

$\bf 4^{10}=(2^2)^{10}=2^{20}\ > \ 2^{15}\ \ ,\\\\2^{15}=32\, 768\ \ ,\ \ 2^{20}=1\, 048\, 576\\\\10^5=(2\cdot 5)^5=2^5\cdot 5^5=100\, 000\\\\2^{15}\ < \ 10^5\ < \ 4^{10}$  

3) Представим  sin410°  как функцию от угла 1 четверти, где  y=sinx - возрастающая функция .

$\bf sin410^\circ =sin(360^\circ +50^\circ )=sin50^\circ \ \ ,\\\\45^\circ \leq 50^\circ \leq 60^\circ \ \ \ \Rightarrow \ \ \ sin45^\circ \leq sin50^\circ \leq sin60^\circ \\\\\dfrac{\sqrt2}{2}\leq sin50^\circ \leq \dfrac{\sqrt3}{2}$  

Ответ: Г) .

Answer 2

Объяснение:

1.

(√3; +∞)

ответ: Д

2.

2¹⁵ ; 4¹⁰ ; 10⁵

2¹⁵ = (2³)⁵ = 8⁵

4¹⁰= (4²)⁵ = 16⁵

10⁵

8<10<16 , значит 8⁵<10⁵<16⁵, следовательно,

2¹⁵ < 10⁵ < 4¹⁰

2¹⁵ ; 10⁵ ; 4¹⁰

ответ: Б

3.

sin410°=sin(360+50)=sin50

sin45≤sin50≤sin60

√2/2≤sin50≤√3/2

[√2/2; √3/2]

ответ: Г