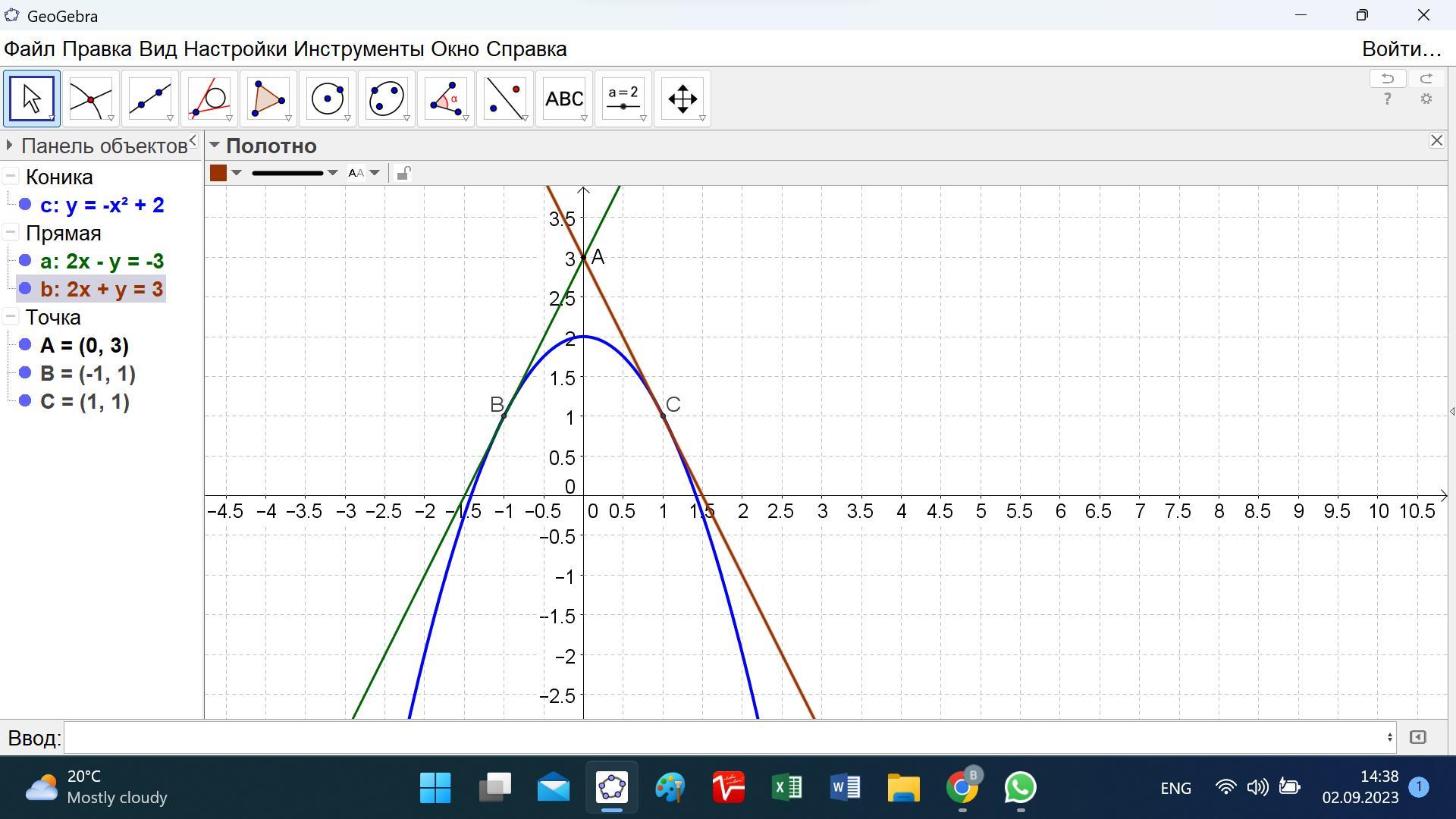
знайдіть площу трикутника, утворенного віссю абсцис і двома дотичними, проведеними з точки (0;3) до графіка функції y = 2-x²
Ответы
Ответ: 4,5 кв. ед.
Пошаговое объяснение:
Решение. Точка А(0; 3) не является точкой касания, так как f(0) не равна ¬3.
1. a – абсцисса точки касания.
2. f(a) = 2 – a2.
3. f '(x) = – 2x , f '(a) = – 2a.
4. y = 2 – a2 – 2a(x – a) – уравнение касательной.
Упростим: y = 2 – a^2 – 2ax +^2 = a^2 – 2ах + 2.
Получаем у = a^2 – 2ах + 2.
Уравнение касательной с угловым коэффициентом:
Касательная проходит через точку А(0; 3), следовательно, ее координаты удовлетворяют уравнению касательной.
3 = a^2 – 2a*0 + 2,
a^2 - 1 = 0, отсюда a1 = – 1, a2 = 1.
Если a = – 1, то уравнение касательной имеет вид у = 1 – 2(-1)х + 2 = 2х + 3.
Если a = 1, то уравнение касательной имеет вид у = 1 – 2*1х + 2 = -2х + 3.
Теперь находим координаты вершин заданного треугольника.
Так как в основании дана ось абсцисс, то ординаты точек равны 0.
Пересечение одной касательной с осью Ох:
0 = 2х + 3, отсюда х = -3/2, для другой 0 = -2х + 3, х =3/2.
Получаем длину основания (3/2) – (-3/2) = 3.
Высота равна длине отрезка ОА = 3.
Ответ: S = (1/2)3*3 = 9/2 = 4,5 кв. ед.