Пожалуйста помогите
даю 50 балов (полная роспись задач)
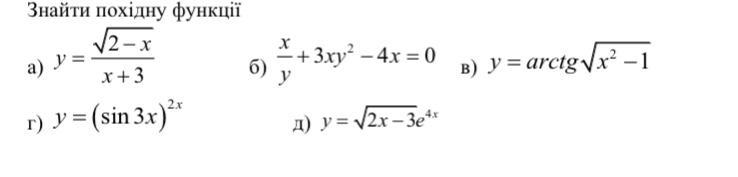
Ответы
Ответ:
Для знаходження похідної функції необхідно застосувати правило диференціювання складеної функції:
(d/dx) (f(g(x))) = f'(g(x)) * g'(x)
Застосуємо це правило до функції y:
y = ((2 - x)^(1/2)) / (x + 3)
f(u) = u^(1/2) - функція, що диференціюється
g(x) = 2 - x - функція, яка є підставою функції f
h(x) = x + 3 - функція, яка є знаменником
Тоді:
y' = [f'(g(x)) * g'(x)] / h(x)
де f'(u) = (1/2)u^(-1/2) - похідна функції f
g'(x) = -1 - похідна функції g
Знаходимо похідні:
f'(u) = (1/2)u^(-1/2)
g'(x) = -1
Підставляємо їх у формулу:
y' = [(1/2)(2 - x)^(-1/2) * (-1)] / (x + 3) + ((2 - x)^(1/2)) / (x + 3)^2
Звідси отримуємо:
y' = -(2 - x)^(-1/2) / (2(x + 3)) + ((2 - x)^(1/2)) / (x + 3)^2
Отже, похідна функції y дорівнює:
y' = -(2 - x)^(-1/2) / (2(x + 3)) + ((2 - x)^(1/2)) / (x + 3)^2