Question

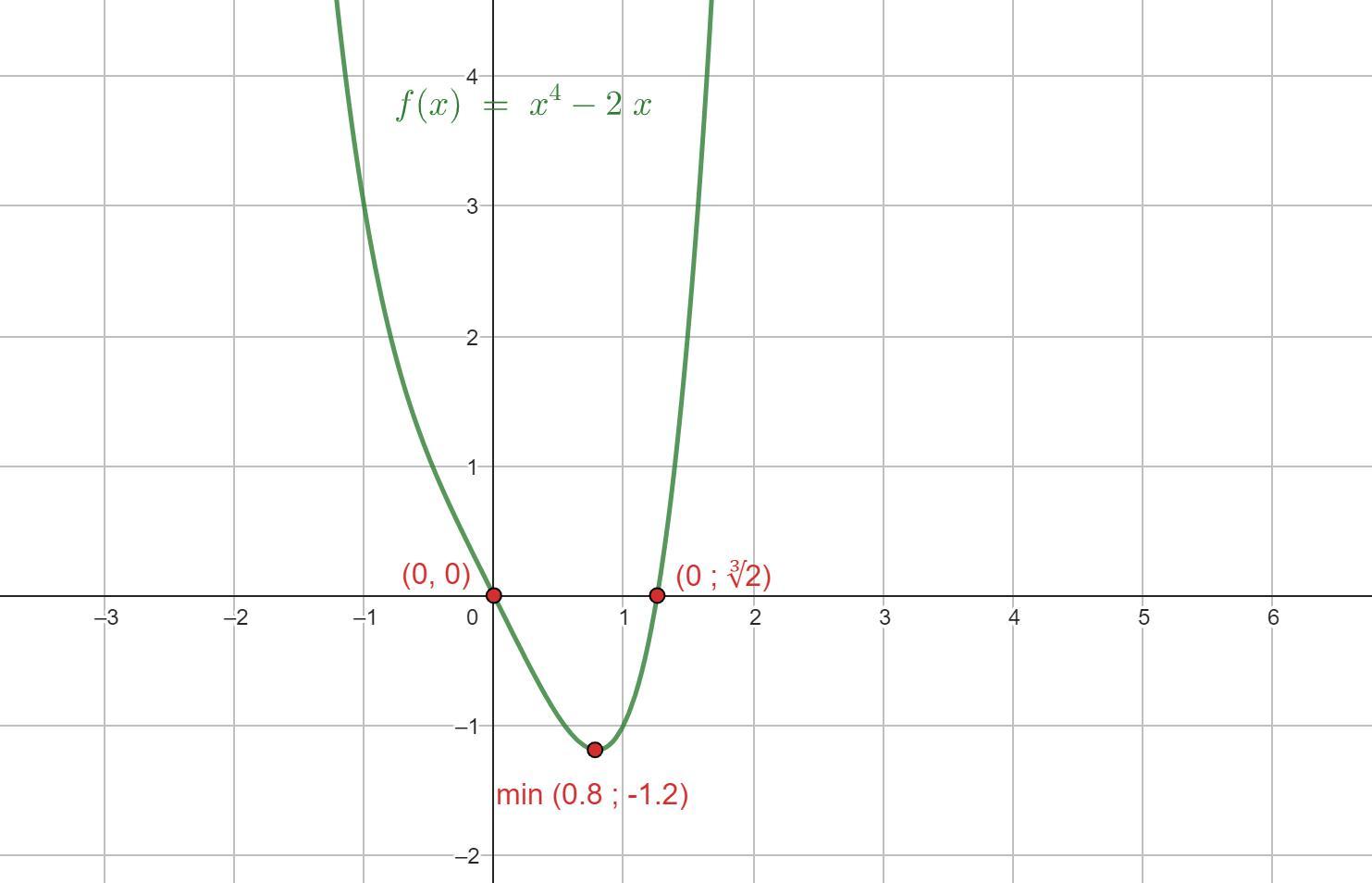
Исследуйте функцию и постройте ее график f(x)=х^4 - 2х

Answer 1

Исследуйте функцию и постройте ее график f(x)=х⁴ - 2х

1. Область определения :

D(y) = R

2.Четность нечетность :

f(-x) = (-x)⁴  -2·(-x)  = x⁴  + 2x ≠ ± f(x) ⇒ функция  не является ни четной ,  ни нечетной

3.Пересечение с осями координат :

Ox ⇒  y = 0

$x^4 - 2x = 0 \\\\ x(x^3 - 2) = 0\\\\x(x-\sqrt[3]{2} )(x^2 +x \sqrt[3]{2} + 1 ) = 0$

$x = 0 ~ , ~ x =\sqrt[3]{2}$

Уравнение

$x^2 +\sqrt[3]{2} x + 1 = 0 \\\\ D = \sqrt[3]{4} - 4 < 0$

Действительных корней не имеет , т.к    D < 0

Oy  ⇒  x = 0

f(0) = 0

4.Непрерывность :

Вертикальных асимптот нет

Находим невертикальную асимптоту

y = kx + b

$\displaystyle k = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{x^4 - 2x}{x} = \lim_{x \to \pm\infty} x^3 - 2 = \pm \infty$  ⇒ невертикальных асимптот нет

5.Возрастание убывание , экстремумы :

f'(x)  = (x⁴  - 2x)' = 4x³  - 2

4x³  -2  = 0

4x³  =   2

$x=\dfrac{1}{\sqrt[3]{2} } = \dfrac{\sqrt[3]{4} }{2} = 0,5 \sqrt[3]{4}$

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(1.2,-0.3) { 0,\!5\sqrt[3]{4} } \put(.5 ,0.1){ \LARGE \text{ ---} } \put(0.6 ,-0.2){ \Large \searrow } \put(2.1 ,0.1){ \Large \text{ +} } \put(1.5,0){\circle*{0.055}} \put(.5 ,0.1){ \LARGE \text{ ---} } \put(2.1 ,-0.2){ \Large \nearrow } \put(0,0){\vector (1,0){3}} \end{picture}$

Возрастает когда  $x \in [~ 0,5\sqrt[3]{4} ~ ; ~ \infty~ )$

Убывает когда       $x \in( - \infty~ ; ~ 0,5\sqrt[3]{4} ~ ]$

Если производная меняет знак c «+» на «-» , то в данной точке будет максимум , если c «-» на «+», то минимум .

$y_{\min} (0,5\sqrt[3]{4} ) = \dfrac{4\sqrt[3]{4} }{16} - 2\cdot 0,5\sqrt[3]{4} = 0,25 \sqrt[3]{4} - \sqrt[3]{4} =-0.75\sqrt[3]{4} \approx-1,2$

При построения графика учтем что $0,5\sqrt[3]{4} \approx 0,8$

6.Выпуклость вогнутость :

Находим вторую производную

f''(x) = (4x³  - 2)' =  12x²

12x² ≥ 0   ⇒ при любом действительном  значении x-са функция всегда вогнута

$\setlength{\unitlength}{23mm}\begin{picture}(1,1) \linethickness{0.2mm} \put(1.45,-0.3) {\sf 0} \put(.5 ,0.1){ \Large \text{ +} } \put(2.1 ,0.1){ \Large \text{ +} } \put(1.5,0){\circle*{0.055}} \put(0,0){\vector (1,0){3}} \end{picture}$