Предмет: Математика,
автор: hdana658
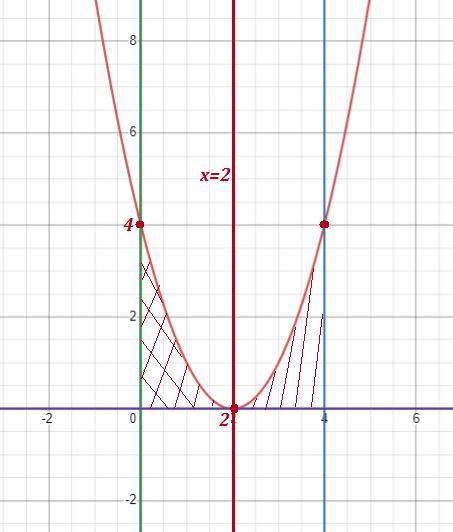
Обчислити об'єм тіла, утвореного обертанням навколо осі Oy y= x^2-4x+4, y=0, x=0, x=4
Ответы
Автор ответа:
1
Ответ:
Область симметрична прямой х=2 , поэтому можно подсчитать объём половины тела и удвоить его .
Уравнение левой ветви параболы : .
Приложения:
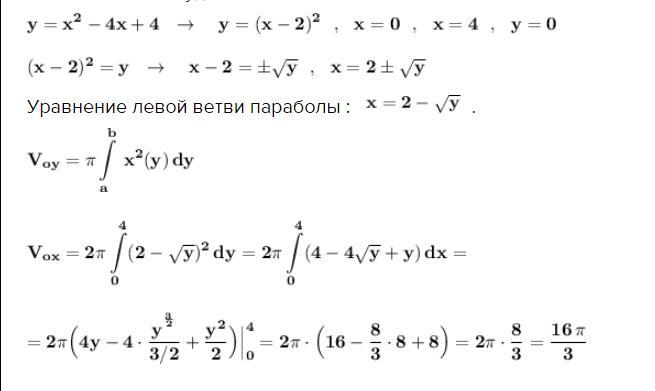
Похожие вопросы
Предмет: Математика,
автор: tfphmptyq2
Предмет: Українська мова,
автор: 32636
Предмет: Биология,
автор: koshtania111
Предмет: Русский язык,
автор: dashachetverus
Предмет: Биология,
автор: prodamakk446