Предмет: Геометрия,
автор: abobusboberys
Це для тебе дякую за допомогу
Приложения:

Ответы
Автор ответа:
2
Ответ:
Периметр ромба равен 20 см.
Объяснение:
Площадь ромба равна 24 см², а одна из его диагоналей 8 см. Найдите периметр ромба.
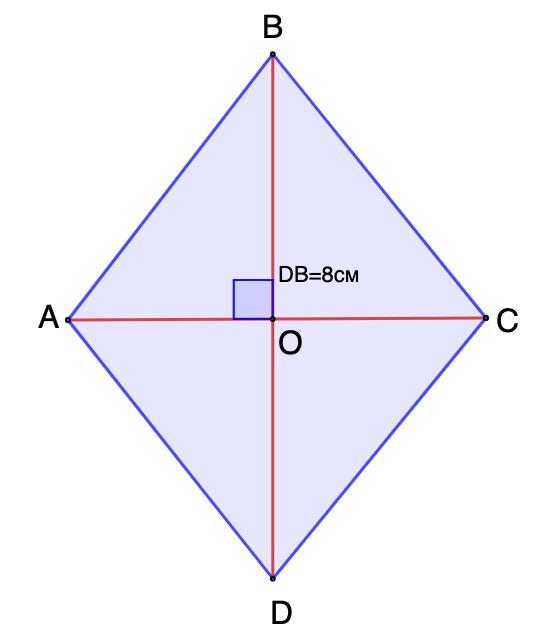
Дано: ABCD - ромб;
S(ABCD) = 24 см²;
BD = см - диагональ.
Найти: Р(ABCD)
Решение:
- Площадь ромба равна половине произведения диагоналей.
- Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
⇒ АС ⊥ BD;
АО = ОС = 6 : 2 = 3 (см); BO = OD = 8 : 2 = 4 (см)
Рассмотрим ΔАВО - прямоугольный;
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
⇒ АВ² = ОВ² + АО² = 16 + 9 = 25 ⇒ АВ = 5 см
- Стороны ромба равны.
⇒ Р(ABCD) = AB · 4 = 5 · 4 = 20 (см)
Периметр ромба равен 20 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: gulnarasaduakasova15
Предмет: Русский язык,
автор: Homak272
Предмет: Геометрия,
автор: EdgarAllanPo
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: Аноним