Question

Abcd ромб, если ac>bd и (ac/bd)-(bd/ac)=2. Найдите угол А.

Answer 1

Ответ:

Угол А равен 45°.

Объяснение:

ABCD - ромб, если AC > BD и (AC/BD)-(BD/AC) = 2. Найдите угол А.

Дано: ABCD - ромб;

AC > BD;

$\displaystyle \frac{AC}{BD}-\frac{BD}{AC}=2$.

Найти: ∠А

Решение:

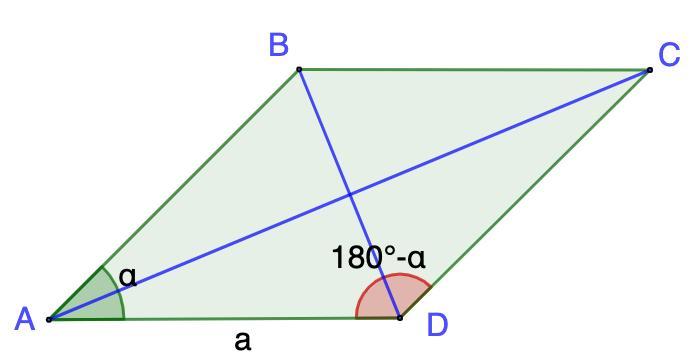
Пусть АВ = ВС = CD = AC = a, ∠A = α

• Сумма углов, прилежащих к одной стороне ромба, равна 180°.

⇒ ∠D = 180° - α.

• По формуле приведения:
• cos (180° - α) = -cos α

• Теорема косинусов:
• Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Из ΔABD:

BD² = AB² + AD² - 2·AB·AD·cos α = a² + a² - 2a²· cos α = 2a²(1 - cos α)

Из ΔACD:

AC² = CD² + AD² - 2·CD·AD·cos (180°-α) = a² + a² + 2a²· cos α =

= 2a²(1 + cos α)

По условию:

$\displaystyle \frac{AC}{BD}-\frac{BD}{AC}=2\\\\\frac{AC^2-BD^2}{BD\cdot AC} =2$

Подставим полученные значения:

$\displaystyle \frac{2a^2(1+cos\;\alpha )-2a^2(1-cos\;\alpha )}{\sqrt{2a^2(1-cos\;\alpha )\cdot2a^2(1+cos\;\alpha )} }=2\\\\\frac{2a^2\cdot 2cos\;\alpha }{2a^2\sqrt{\underbrace{1-cos^2\alpha }_{sin^2\alpha }} }=2 \\\\\frac{cos\;\alpha }{|sin\;\alpha |} =1$

Так как α - острый угол, то sin α > 0.

$\displaystyle \frac{cos\;\alpha }{sin\;\alpha }=ctg\;\alpha$

⇒ ctg α = 1   ⇒ α = 45°

Угол А равен 45°.

#SPJ1