Терміново, будь ласка, допоможіть !! не з чатуджпт
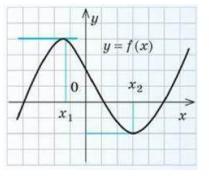
На рисунку зображено графік функції y = f(x) та дотичні до нього в точках з абсцисами x1 і x2. Користуючись геометричним змістом похідної, записати значення виразу f'(x1) * f'(x2)
Ответы
Ответ: Для того, щоб записати значення виразу f'(x1) * f'(x2), потрібно спочатку знайти похідні функції у точках x1 та x2.
З геометричного змісту похідної можна отримати, що похідна f'(x) функції y = f(x) в точці x дорівнює нахилу дотичної до графіку функції у точці x.
Отже, якщо ми маємо графік функції y = f(x) та дотичні до нього у точках x1 та x2, то можна знайти похідні f'(x1) та f'(x2) шляхом обчислення нахилів дотичних.
Після знаходження значень f'(x1) та f'(x2) можна записати значення виразу f'(x1) * f'(x2) та проінтерпретувати його як показник нахилу прямокутника, побудованого на дотичних до графіку функції у точках x1 та x2. Іншими словами, чим більше значення виразу f'(x1) * f'(x2), тим більш прямокутник, побудований на дотичних, буде високий і широкий, тобто функція буде масти велику зміну в обох точках x1 та x2.
Загальна формула для знаходження похідної функції y = f(x) за визначенням:
f'(x) = lim(h -> 0) [(f(x + h) - f(x)) / h]
Для знаходження нахилу дотичної до графіку функції у точці x можна скористатись формулою:
y - f(x) = f'(x) * (x - x)
За цією формулою можна знайти рівняння дотичної до графіку функції у точках x1 та x2, з яких можна знайти похідні f'(x1) та f'(x2).
Отже, значення виразу f'(x1) * f'(x2) можна обчислити, знаючи рівняння дотичних до графіку функції у точках x1 та x2, тобто нахил дотичної у кожній точці буде дорівнювати похідній f'(x1) або f'(x2), а отже, значення виразу f'(x1) * f'(x2) можна записати як добуток двох нахилів дотичних до графіку функції у точках x1 та x2.
Формула для знаходження нахилу дотичної до графіку функції у точці x виглядає так:
f'(x) = lim(h -> 0) [(f(x + h) - f(x)) / h]
Застосувавши цю формулу до точок x1 та x2, ми можемо знайти значення похідних f'(x1) та f'(x2). Потім, підставивши ці значення у формулу f'(x1) * f'(x2), ми отримаємо значення виразу.
Отже, щоб продовжити, потрібно знайти похідні f'(x1) та f'(x2) та обчислити їх добуток. Це можна зробити за допомогою формули для похідної, описаної вище, та рівняння дотичних до графіку функції у точках x1 та x2. Після знаходження значення виразу f'(x1) * f'(x2) можна проінтерпретувати його як показник нахилу прямокутника, побудованого на дотичних до графіку функції у точках x1 та x2.
Надеюсь помог:)