Предмет: Геометрия,
автор: imangalim2008
1. Из одной точки к окружности проведены касательная и секущая. Найти секущую, если известно, что внутренний отрезок относится к внешнему как 3:1. Длина касательной 12 см.
Ответы
Автор ответа:
0
Ответ:
24 см
Объяснение:
Квадрат касательной равен произведению секущей на её внешнюю часть.
Пусть внутренний отрезок секущей 3х см, внешний х см., тогда
12² = (3х+х)*х
144=4х²
х²=36
х=6
Внешний отрезок секущей 6 см, внутренний 3*6=18 см.
Секущая имеет длину 6+18=24 см.
Приложения:

ildar502020:
Пеппер! Здравствуйте! У Вас ошибка: AC=3x+x=4x, так как AC=1x; CD=3x!!!
Спасибо, понял.
Автор ответа:
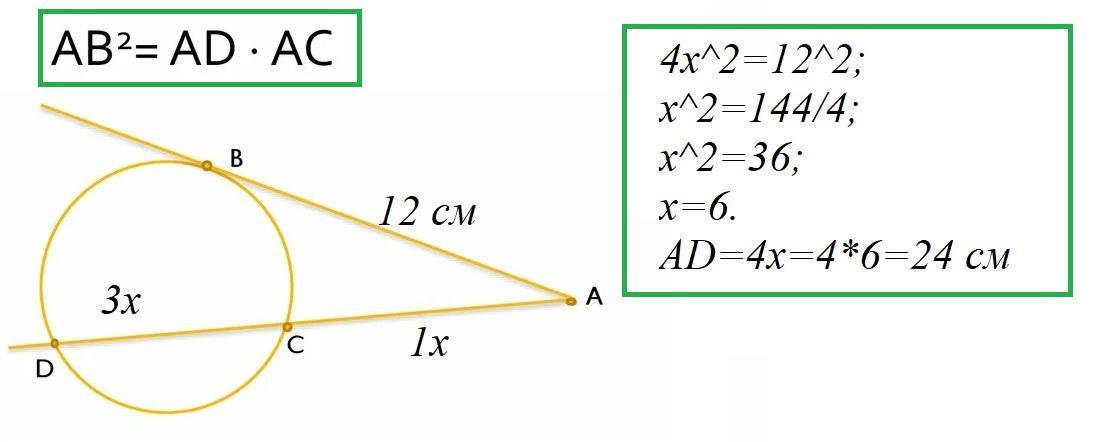
1
Ответ: 24 см.
Объяснение:
Дано
AB=12 см - касательная
AD - секущая
AC:CD = 1:3
------------
AD=?
Известно, что AB²=AD*AC. Тогда
12²=4x*x, где x- одна часть секущей AD.
4x²=144;
x²=36;
x=±6 => -6 - не соответствует условию
x=6.
Секущая AD=3x+x=4x = 4*6 = 24 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: super2016alser
Предмет: Українська мова,
автор: karinabilenka820
Предмет: Алгебра,
автор: suiuntbekovvadaku
Предмет: Русский язык,
автор: tynaeverlan33
Предмет: История,
автор: kravchukdima159