5.51 помогите с решением
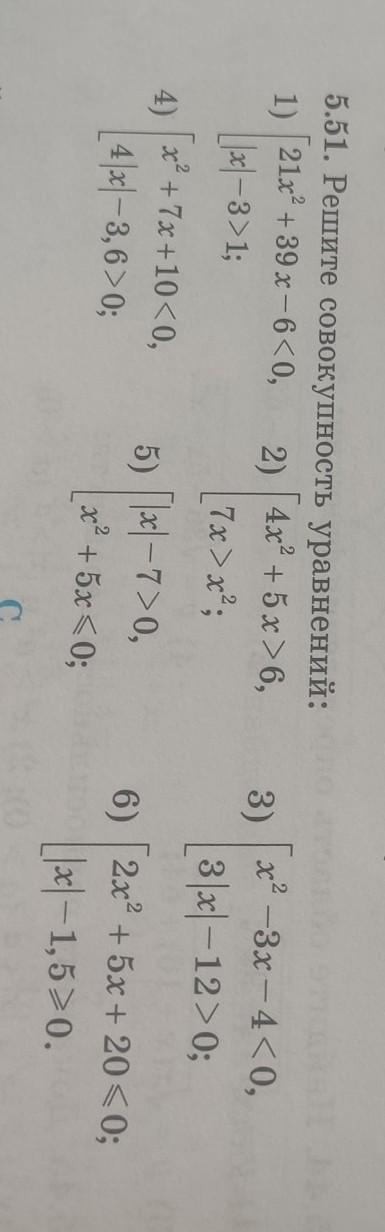
Ответы
Ответ:
To solve this inequality, we need to find the values of x that make the expression less than zero. We can do this by factoring the expression or by using the quadratic formula, but in this case, we can also use a shortcut:
1. Find the roots of the expression by setting it equal to zero: 21x²+39x-6=0
We can factor this expression as (3x-1)(7x+6)=0
Therefore, the roots are x=1/3 and x=-6/7
2. Plot these roots on a number line:
-6/7 1/3
|-------|-------|
A B
3. Test a value in each interval to see if the expression is less than zero:
-7 -1 0 1/2 1 2
|-----------|-------|-----------|--------|--------|
+ - - +
C D E F
For interval A (-∞,-6/7), we can test x=-1:
21(-1)²+39(-1)-6 = -24 < 0
Therefore, interval A is part of the solution.
For interval B (-6/7,1/3), we can test x=0:
21(0)²+39(0)-6 = -6 < 0
Therefore, interval B is part of the solution.
For interval C (-∞,-1), we can test x=-2:
21(-2)²+39(-2)-6 = 12 > 0
Therefore, interval C is not part of the solution.
For interval D (-1,0), we can test x=-1/2:
21(-1/2)²+39(-1/2)-6 = -13/4 < 0
Therefore, interval D is part of the solution.
For interval E (0,1/3), we can test x=1/4:
21(1/4)²+39(1/4)-6 = -15/16 < 0
Therefore, interval E is part of the solution.
For interval F (1/3,∞), we can test x=2:
21(2)²+39(2)-6 = 138 > 0
Therefore, interval F is not part of the solution.
4. Combine the intervals that make the expression less than zero:
(-∞,-6/7) U (-1,0) U (0,1/3)
Therefore, the solution to the inequality is x ∈ (-∞,-6/7) U (-1,0) U (0,1/3).