Знайти cos С у трикутнику АВС,
якщо А(1;5) ; В(4;1); С(7; 3).
Ответы
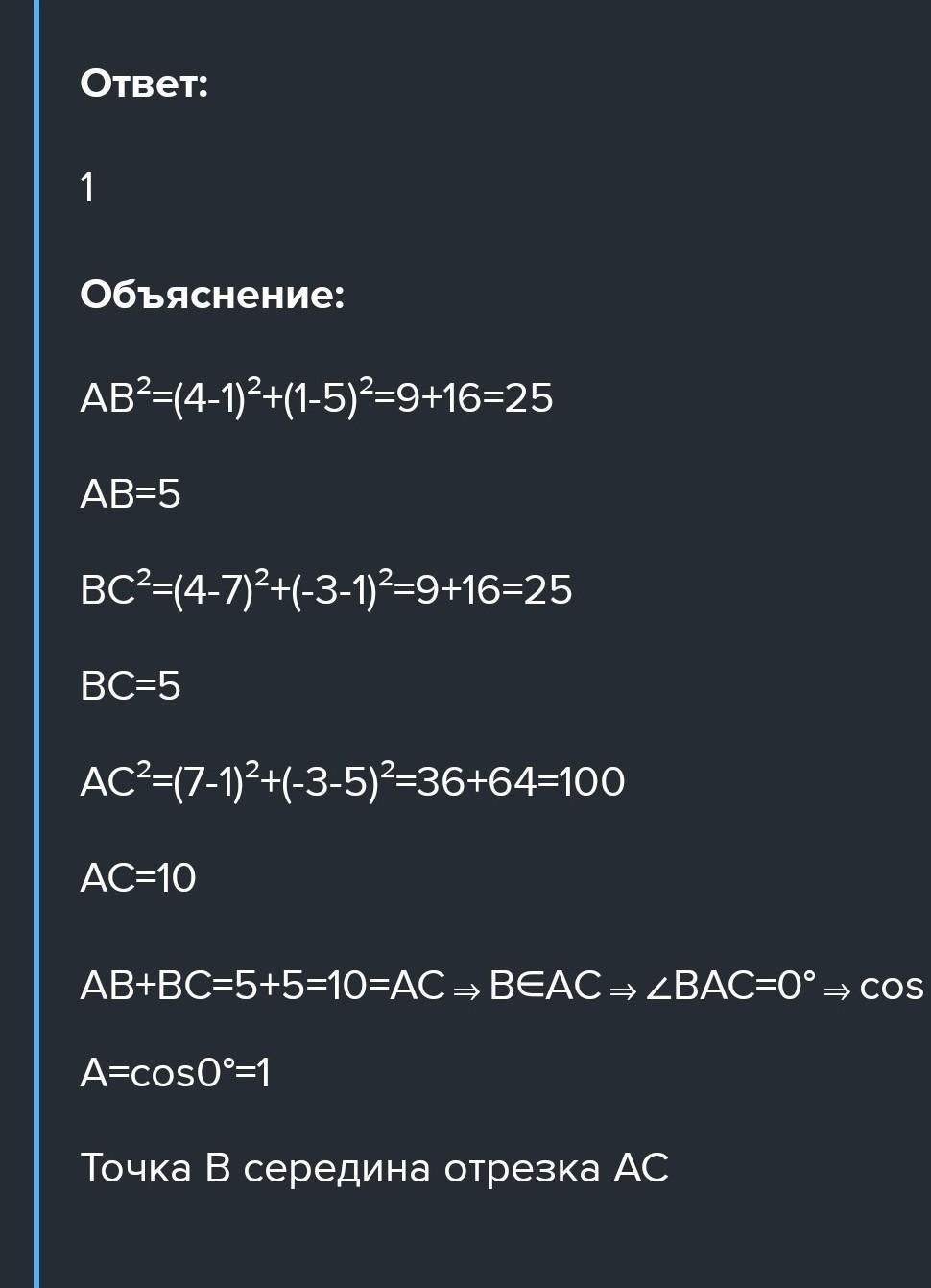
Ответ:
Надеюсь поможет.............
Для розв'язання задачі нам потрібно визначити довжини всіх сторін трикутника і використати формулу косинуса для кута C.
Відстань між двома точками можна визначити за допомогою формули відстані між двома точками у просторі:
d = √((x2 - x1)² + (y2 - y1)²)
Тоді довжини сторін трикутника можна обчислити наступним чином:
AB = √((4 - 1)² + (1 - 5)²) = √(3² + (-4)²) = √25 = 5
AC = √((7 - 1)² + (3 - 5)²) = √(6² + (-2)²) = √40
BC = √((7 - 4)² + (3 - 1)²) = √(3² + 2²) = √13
Застосовуючи формулу косинуса для кута C, отримаємо:
cos C = (AB² + AC² - BC²) / (2 * AB * AC)
cos C = (5² + √40² - √13²) / (2 * 5 * √40)
cos C = (25 + 40 - 13) / (10√40)
cos C = 52 / (10√40)
Звідси можна спростити дріб, помноживши чисельник і знаменник на √40:
cos C = (52 / 10) * (√40 / 40)
cos C = 13 / 5√10
Отже, cos C дорівнює 13 / 5√10. Це можна ще подальше спростити, помноживши чисельник і знаменник на √10:
cos C = (13√10) / (5 * 10)
cos C = (13√10) / 50
Тому cos C дорівнює (13√10) / 50.
Як зміг так розвязав