допоможіть прошууу даю 85 балів
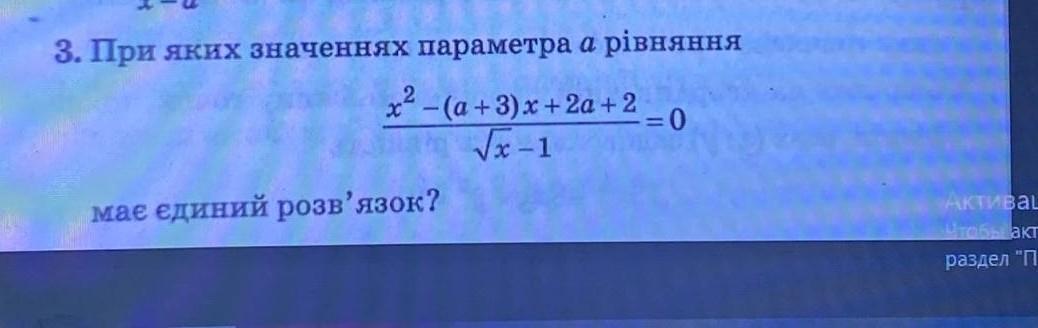
Ответы
Ответ:
Для розв'язання цієї задачі спочатку потрібно зрозуміти, за яких умов рівняння може мати один розв'язок.
Згідно з теорією, рівняння має один розв'язок, якщо дільник у чисельнику і дільник у знаменнику рівні одне одному в точці розв'язку.
Таким чином, ми повинні знайти значення параметра a, при яких дільник у чисельнику і дільник у знаменнику рівні одне одному у точці розв'язку.
Розглянемо чисельник рівняння:
x ^ 2 - (a + 3) * x + 2a + 2
Знайдемо його корені:
x1 = (-(-a - 3) - sqrt((a + 3)^2 - 8(2a + 2))) / 2
x2 = (-(-a - 3) + sqrt((a + 3)^2 - 8(2a + 2))) / 2
Якщо чисельник рівняння має один корінь, то це означає, що дискримінант дорівнює нулю:
(a + 3)^2 - 8(2a + 2) = 0
Розв'язавши це рівняння, ми отримаємо:
a = 5 або a = -11
Таким чином, рівняння має один розв'язок при a = 5 або a = -11.
Надеюсь правильно:)