Question

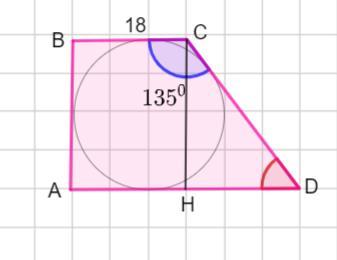
В прямоугольную трапецию вписана окружность с радиусом равным 19. Найди площадь данной трапеции, если её меньшее основание равно 18, а один из углов равен 135°.
СРОЧНО НУЖНО РЕШЕНИЕ, СПАСИБО

Answer 1

Ответ:

1 406 кв. ед.

Пошаговое объяснение:

В прямоугольную трапецию вписана окружность радиуса 19. Найти площадь данной трапеции, если ее меньшее основание 18, а один из углов равен 135°.

Пусть дана прямоугольная трапеция АВСD . ВС = 18 ед. , ∠ С =135 °.

В трапецию вписана окружность. Если радиус окружности равен 19 ед., то высота трапеции СН = 2 ·19 = 38 ед.

∠С  и ∠D внутренние односторонние при ВС ║АD и секущей СD.

Тогда ∠С  + ∠D = 180°. Отсюда ∠D = 180° - 135° = 45°.

Рассмотрим ΔСНD - прямоугольный. Сумма острых углов прямоугольного треугольника равна  90°.

Тогда ∠НСD = 90°- 45°=45°.

Если в треугольнике два угла равны, то он равнобедренный.

Значит, ΔСНD - равнобедренный .

НD= СН = 38 ед.

АD =АН +НD

АВСН - прямоугольник ; АН = ВС = 18 ед.

АD = 18 +38 = 56 ед.

Площадь трапеции равна произведению полусуммы оснований на высоту .

$S =\dfrac{BC +AD }{2} \cdot CH;\\\\S =\dfrac{18 +56 }{2} \cdot 38=\dfrac{74}{2} \cdot 38=37 \cdot 38= 1406$

Значит, площадь трапеции равна 1 406 кв. ед.

#SPJ1