Предмет: Геометрия,
автор: angeliwes
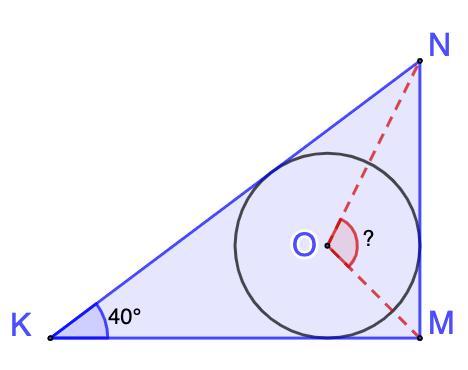
5.O-центр кола вписаного в прямокутний трикутник KMN 3 гіпотенузою KN, в якому Кут MKN = 40°. Знайдіть градусну міру кута MON.
СРОЧНО С РИСУНКОМ (7 КЛАС)
Ответы
Автор ответа:
4
Ответ:
Угол MON равен 110°.
Объяснение:
5. О - центр окружности, вписанной в прямоугольный треугольник KMN 3 гипотенузой KN, в котором угол MKN = 40°. Найдите градусную меру угла MON.
Дано: ΔKMN - прямоугольный.
Окр.О - вписана в ΔKMN;
∠MKN = 40°
Найти: ∠MON
Решение:
Рассмотрим ΔMKN - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠N = 90° - ∠MKN = 90° - 40° = 50°
- Центр вписанной окружности лежит на биссектрисе угла.
⇒ ∠KNO = ∠ONM = 50° : 2 = 25°;
∠KMO = ∠OMN = 90° : 2 = 45°
Рассмотрим ΔONM.
- Сумма углов треугольника равна 180°.
⇒ ∠MON = 180° - ∠OMN - ∠ONM = 180° - 45° - 25° = 110°
Угол MON равен 110°.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: dermor7777777
Предмет: Математика,
автор: misterfirs
Предмет: Химия,
автор: sofialavrentiva941
Предмет: Українська мова,
автор: nikitagoriskij4
Предмет: Русский язык,
автор: Юлия8906