Question

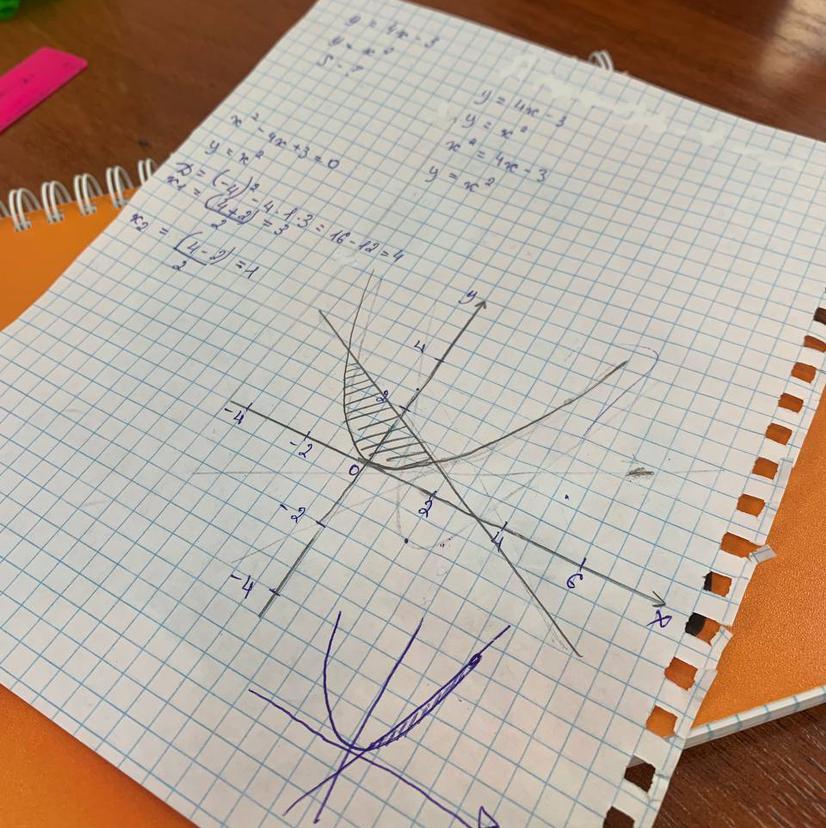
Найдите площадь между ограниченными линиями, пожалуйста.
у=4х-3
у=х ^2
-?

Answer 1

Ответ:      1 1/3  кв. ед.

Объяснение:

у=4х-3;

у=х^2;

1)  Строим графики функций (См. скриншот)

2) Площадь криволинейной трапеции находим по формуле Ньютона-Лейбница

S=S(ABmCD) - S(ABnCD) = ∫ₐᵇf₁(x)dx - ∫ₐᵇf₂(x)dx.

3) По графику определяем пределы интегрирования: а=1 b=3.

Тогда S=∫₁³f₁(x)dx - ∫₁³f₂(x)dx =  ∫₁³(4x-3)dx - ∫₁³(x²)dx;

4)  ∫₁³(4x-3)dx = 4∫₁³(x)dx -3∫₁³(1)dx = 4(x²/2)|₁³-3x|₁³ = 4(9/2 - 1/2) -3(3-1) =

=4*4-6=10 кв. ед.

5)  ∫₁³(x²)dx = x³/3|₁³ = 1/3(27-1) = 26/3 =8 2/3  кв. ед.

6) S=10-8 2/3 = 1 1/3  кв. ед.