Предмет: Алгебра,
автор: toliooldtt
Дослідіть функцію у = х^4 - 4х^2 та побудуйте її графік
Приложения:
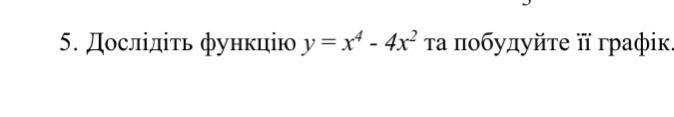
Ответы
Автор ответа:
0
Ответ:
Функция четная:
y(–x)=(–x)4–4·(–x)2=x4–4x2=y(x)
y`=4x3–8x
y`=0
4x3–8x=0
4x·(x2–2)=0
x=0 или x= ± √2 – точки возможного экстремума.
Применяем достаточное условие, т.е проверяем знак производной:
__–_ (–√2) __+___ (0) ___–___ ( √2) __+___
y`<0 ⇒ функция убывает на (– ∞ ;–√2) и на (0; √2)
y`> 0 ⇒ функция возрастает на (–√2; 0) и на (√2; + ∞ )
x= ± √2 – точки минимума, производная меняет знак с – на +
y(± √2 )=(± √2 )4–4·(± √2 )2=4–4·2=–4
x=0 – точка максимума, производная меняет знак с + на –
y(0)=0
y``=(4x3–8x)`
y``=12x2–8
y``=0
12x2–8=0
3x2–2=0
x= ± √2/3 – точки перегиба, вторая производная при переходе через точки меняет знак:
_+_ ( –√2/3) __–__ ( √2/3) __+__
Функция выпукла вниз на (–√2/3; √2/3)
выпукла вверх на (– ∞ ;–√2/3) и на (√2/3; + ∞ )
Объяснение:
Похожие вопросы
Предмет: Українська мова,
автор: kovalenkokosta66
Предмет: Физика,
автор: antonmorozkart
Предмет: Химия,
автор: zavalida
Предмет: История,
автор: Аноним
Предмет: Музыка,
автор: Gighh