Предмет: Геометрия,
автор: artempro32334
У трапецію вписано коло радіусом 4 см. Бічні сторони трапеції дорівнюють 12 см і 10 см. Знайдіть площу трапеції.(У відовідь записати число без одиниць вимірювання)
Ответы
Автор ответа:
6
Ответ:
88
Объяснение:
В трапецию вписана окружность радиуса 4 см . Боковые стороны трапеции равны 12 см и 10 см. Найти площадь трапеции.
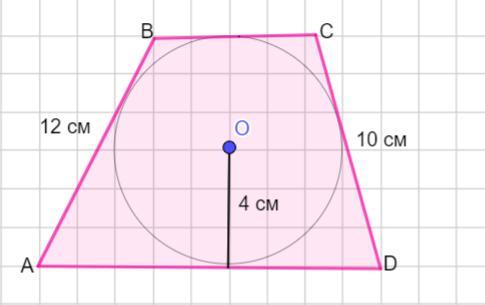
Пусть дана трапеция АВСD. АВ = 12 см, СD = 10 см.
В трапецию вписана окружность радиуса 4 см. Тогда высота трапеции равна h = 4 · 2 = 8 см.
Если окружность вписана в четырехугольник, то суммы противолежащих сторон равны.
Значит, BC + AD = AB +CD
BC + AD = 12 +10 = 22 cм
Площадь трапеции равна произведению полусуммы оснований на высоту
где a и b - основания трапеции, h - высота трапеции
Значит, площадь трапеции равна 88 см ².
#SPJ1
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: ilacurar
Предмет: Физика,
автор: murk76056
Предмет: История,
автор: erbosynmaulen
Предмет: Алгебра,
автор: nkv2181219