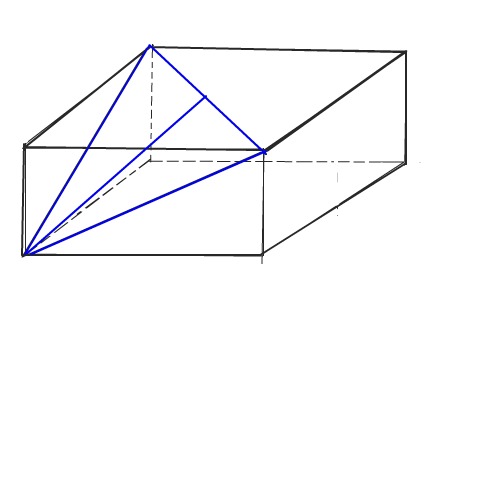
Помогите пожалуйста решить, очень срочно надо. Боковая поверхность правильной четырехугольной призмы имеет площадь 16 дм2. Диагональ основания призмы равна 4 корня из 2 дм. Найдите площадь сечения призмы, проходящего через диагонали двух смежных боковых граней, имеющие общую вершину.
Ответы
Формула диагонали квадрата - а√2, значит,
сторона основания равна 4 дм.
Площадь одной грани призмы 16:4=4.
Поэтому ее высота равна
Н= 4:4=1 дм.
Зная высоту и длину стороны боковой грани, находим ее диагональ:
d²=4²+1²=17
d=√17
Высоту получившегося равнобедренного треугольника
со сторонами √17 и основанием, равным диагонали квадрата (основания) 4√2
найдем из половины этого треугольника:
Эта половина - прямоугольный треугольник с гипотенузой √17 и основанием 2√2
h²=( √17)² - (2√2)²=17-8=9
h= √9=3 дм
Площадь сечения
S=(3*4√2):2=6√2 дм²