Предмет: Геометрия,
автор: sofia9056
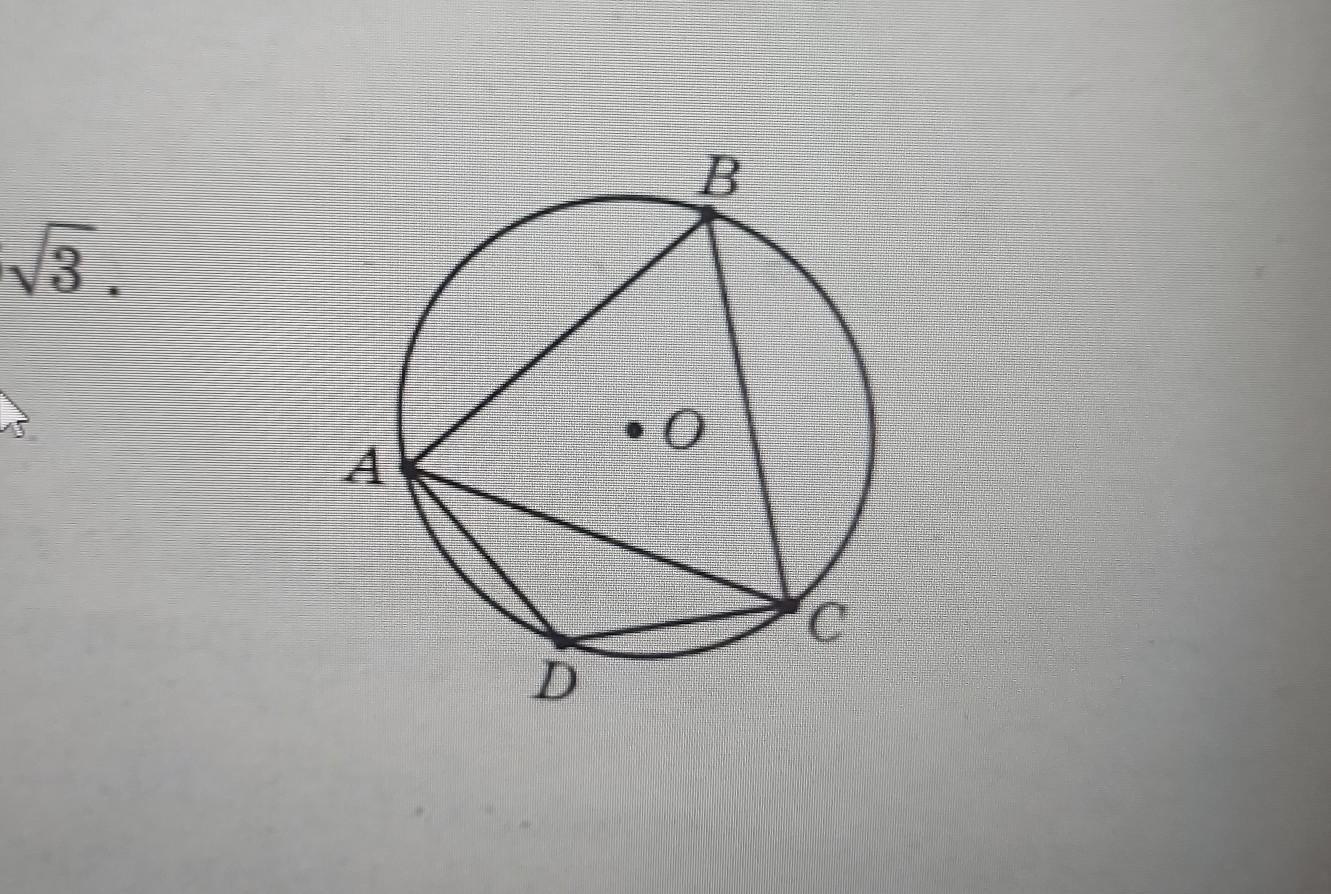
на рисунку зображено коло із центром у точці О, AC дорівнює 6 корінь з трьох знайдіть радіус кола якщо дуга AC дорівнює 120°
Приложения:
Ответы
Автор ответа:
2
Ответ:
6 ед.
Объяснение:
На рисунке изображена окружность с центром в точке О, АС = 6√3. Найти радиус окружности , если дуга Ас равна 120.
На рисунке изображен ΔАВС - вписанный в окружность. Сторона АС =6√3. ∠АВС - вписанный и опирается на дугу АС.
Так как вписанный угол равен половине дуги, на которую он опирается, то ∠АВС = 120 ° : 2 = 60 °.
Радиус окружности, описанной около треугольника, определяется по формуле:
где α - угол, противолежащей стороне а.
Тогда
Значит, радиус окружности, описанной около треугольника АВС равен 6 ед.
#SPJ1
Похожие вопросы
Предмет: География,
автор: anisannn
Предмет: Физика,
автор: erbolatulyalihan42
Предмет: Математика,
автор: romanovanastya8567
Предмет: Геометрия,
автор: lebedevadiana66
Предмет: География,
автор: bibig0mbibi