Предмет: Геометрия,
автор: nnnasstyaaa
ДАЮ 100 БАЛІВ! знайдіть всі значення параметра а при кожному з яких рівняння a²cos4πx+a|x|=1 має єдиний розв'язок.
Ответы
Автор ответа:
1
Відповідь:
а=-1
Пояснення:
a²cos4πx+a|x|=1
якщо x₁ - корінь, то х₂=-х₁ також буде коренем
тому єдиний корінь х=0
тоді
a²cos(4π*0)+a|0|=1
a²+0=1
a²=1
а=±1
але це ще не все
х = 0 - корінь рівняння cos4πx+|x|=1 та корінь рівняння cos4πx-|x|=1
але чи єдиний ?
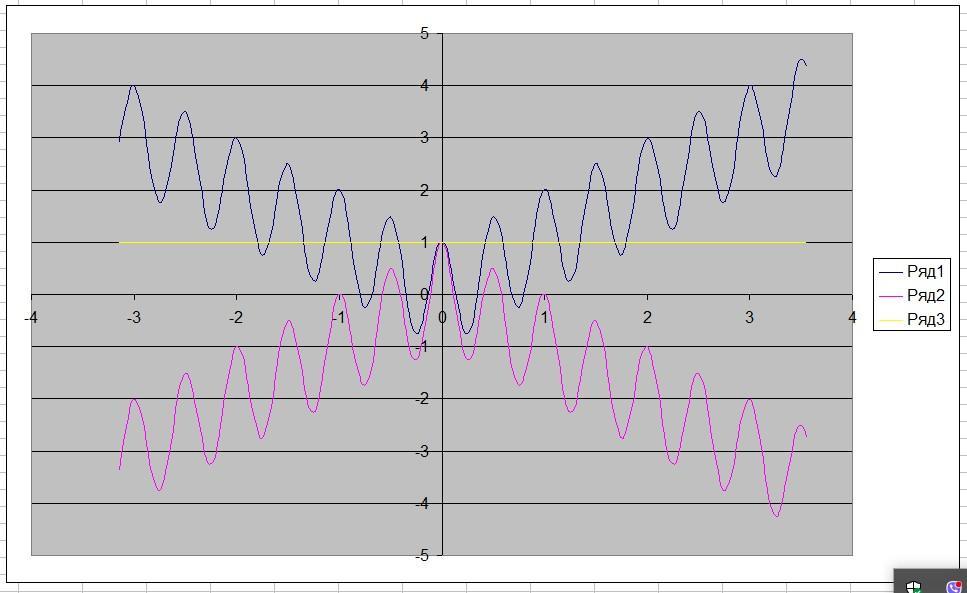
при а=1 - рівняння a²cos4πx+a|x|=1 має 15 коренів
у=cos4πx+|x| - (синім кольором) перетинається з прямою у=1 (жовтим кольором) в 15 точках
при а=-1 - рівняння a²cos4πx+a|x|=1 має єдиний корінь
у=cos4πx-|x| - (червоним кольором) перетинається з прямою у=1 (жовтим кольором) в 1 точці. - а=-1 - це відповідь
Приложения:
Автор ответа:
1
Відповідь: фото
Пояснення:
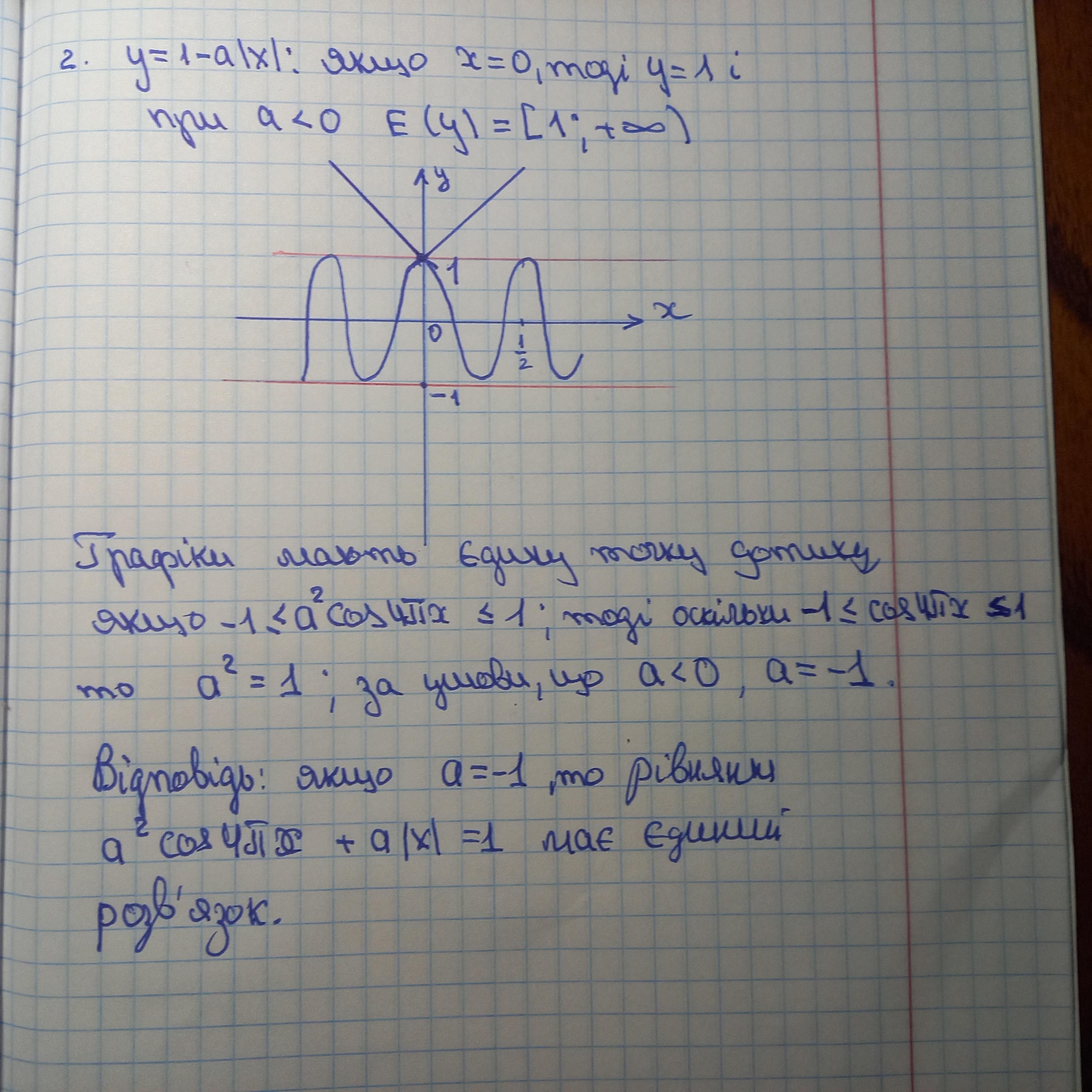
якщо бачимо модуль, то спробуємо графічний спосіб.
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: sdweroyt
Предмет: Алгебра,
автор: amanovnurtas15
Предмет: Английский язык,
автор: 123890qweiop
Предмет: Математика,
автор: andrijkuzo1997
Предмет: Алгебра,
автор: migovichroman28