Предмет: Алгебра,
автор: jdkdihhjs
Помогите!!!!!!!!
Пужалуйста
Приложения:
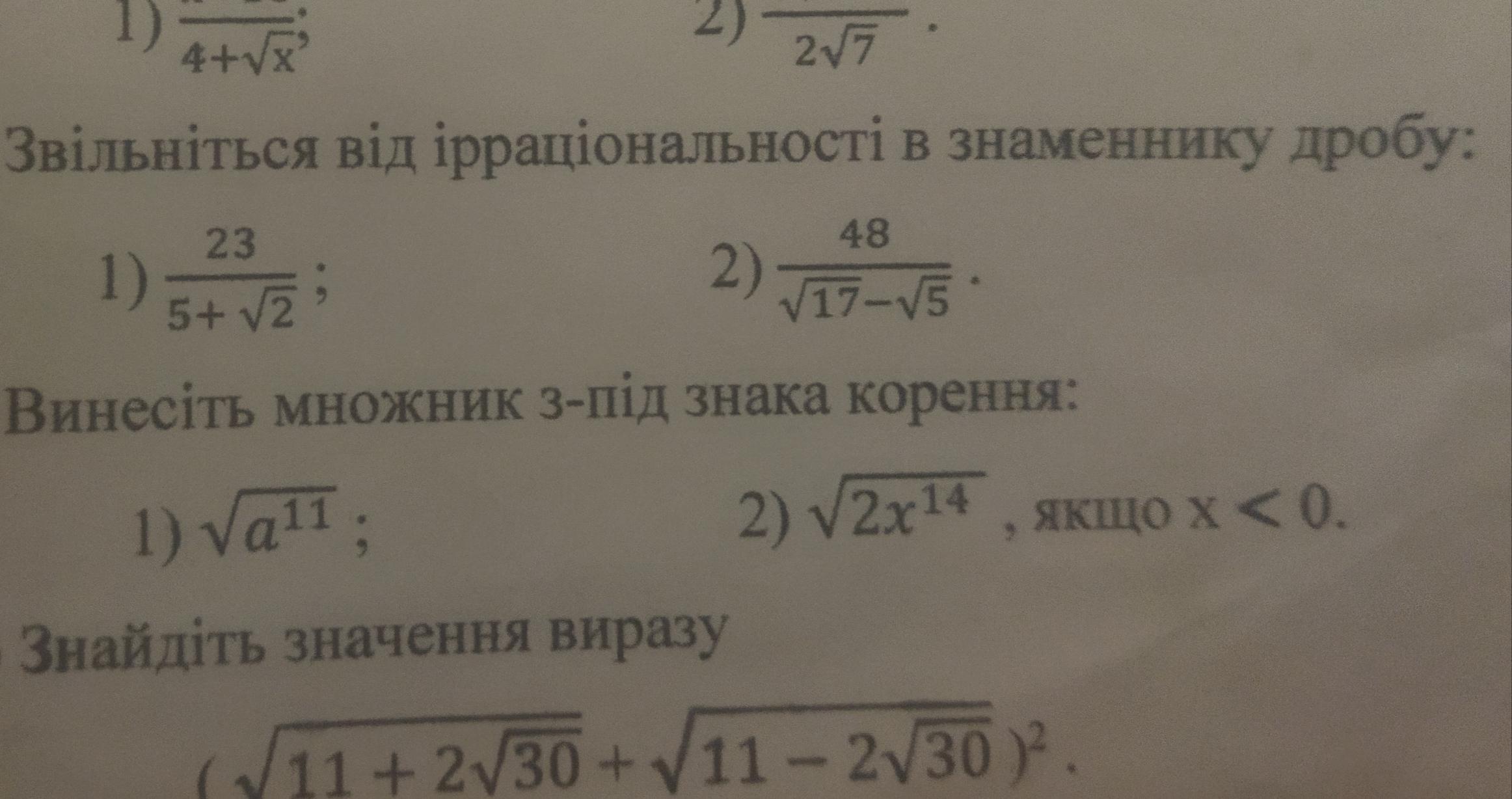
Ответы
Автор ответа:
0
Задання 1.
1)
2)
Завдання 2.
1) З умови випливає, що а>=0. Тоді
2) Якщо х<0
Завдання 3.
Похожие вопросы
Предмет: Английский язык,
автор: QunRoty
Предмет: Математика,
автор: robiyausmonova310
Предмет: Алгебра,
автор: ramazanutarbaev6
Предмет: Информатика,
автор: SOPHIAOBUKHOVA
Предмет: Другие предметы,
автор: rakcheevkiriill