Question

помогите пожалуйста ​

Answer 1

Ответ:

1) 5√2 см

2)5 см

3) 10см

Решение:
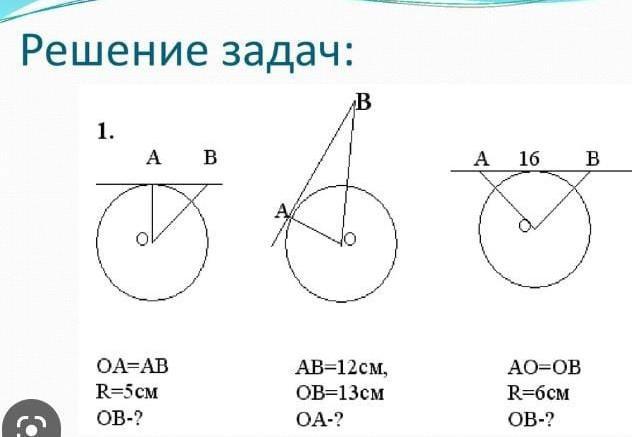
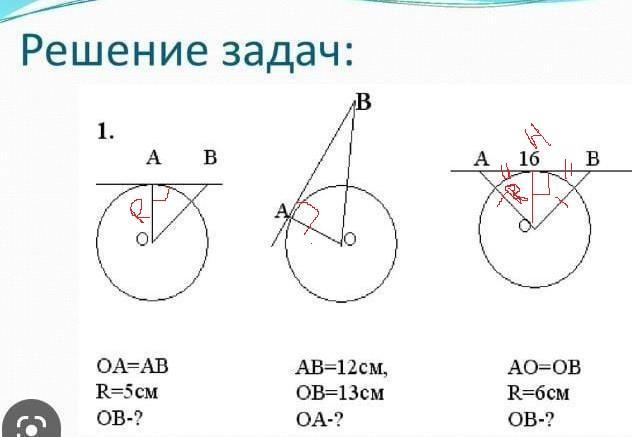
1) Рассмотрим ΔОАВ, ∠А=90°, как  касателная к радиусу, ОА=АВ=R=5см,
По теореме Пифагора ОВ²=ОА²+АВ²=2R²=2*5²=50(cм²)

$OB=\sqrt{50}=\sqrt{25*2}=5\sqrt{2}$(см)

2)АО⊥АВ, как касательная к радиусу окружности в точке касания
Рассмотрим ΔОАВ, ∠А=90°.
По теореме Пифагора
ОВ²=АВ²+ОА² → ОА²=ОВ²-АВ²

$OA=\sqrt{13^2-12^2} =\sqrt{(13-13)(13+12)} =\sqrt{25}=5$(cм)

3) Рассмотрим ΔАОВ- равнобедренный( ОА=ОВ).Проведём ОН⊥АВ, ОН=R.
Согласно свойству высоты, проведённуюк основанию равнобедренного треугольника, ОН- медиана стороны АВ, следовательно АН=ВН=1/2АВ=16:2=8(см)
Рассмотрим ΔОНВ, где ∠Н=90°,ОН=R=6 см, НВ=8 см.
Согласно теореме Пифагора ОВ²=ОН²+НВ²
$OB=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$(cм)