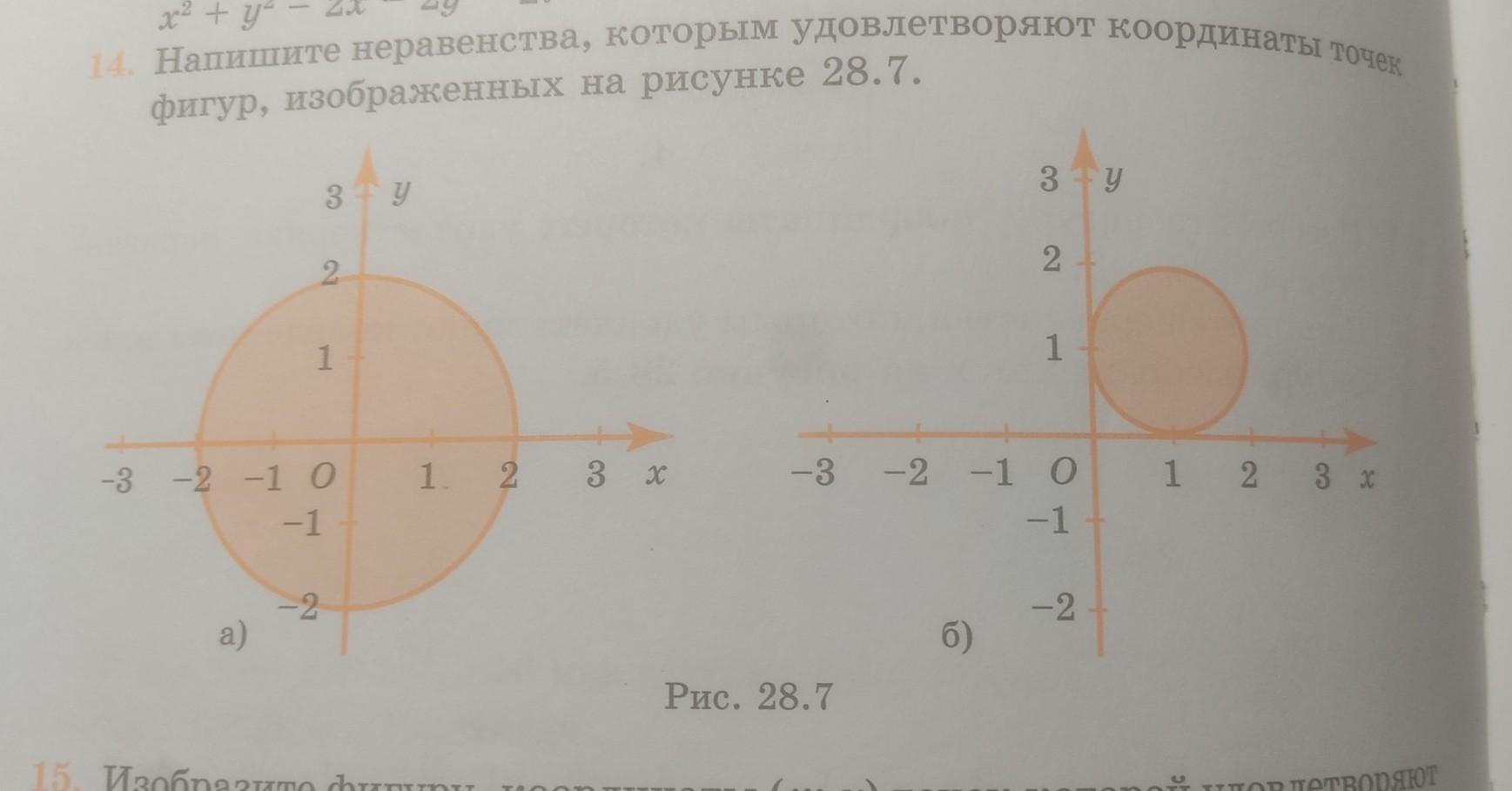
Напишите неравенства, которым удовлетворяют координаты точек фигур, изображенных на рисунке 28.7
СРОЧНО!!!
Ответы
Ответ:
а) x² +y²≤ 4; б) (x-1)² +(y-1)²≤ 1.
Объяснение:
а) Рассмотрим первый рисунок. На рисунке изображен круг . Составим уравнение окружности, ограничивающей этот круг.
, где (a; b) - центр окружности , R - радиус окружности - уравнение окружности в общем виде.
На рисунке мы видим, что центр окружности в начале координат, то есть в точке (0; 0) . Тогда уравнение окружности будет x² +y²= R².
Радиус окружности R=2 и тогда уравнение окружности x² +y²= 4.
Составим неравенство, так чтобы все точки заштрихованной области удовлетворяли неравенству.
Точка (0; 0 ) принадлежит кругу . 0² +0² < 4 так как окружность на рисунке зачерчена сплошной линией , то неравенство , которому удовлетворяют все точки на первом рисунке будет x² +y²≤ 4
б) На втором рисунке изображена окружность с центром в точке
(1; 1) и радиуса, равного 1.
Тогда уравнение окружности принимает вид (x-1)² +(y-1)²= 1. Так как все точки должны принадлежать кругу, ограниченной этой окружностью и сама окружность изображена сплошной линией, то все точки, которые изображены на втором рисунке будут удовлетворять неравенству (x-1)² +(y-1)²≤ 1.
#SPJ1