Предмет: Алгебра,
автор: Аноним
Помогите пж дам 50 баллов
3. Упростите выражение:
а)
sin a+sin a11+cosa 1-cosa. 1+ctg² a б) (1+ cos 2a)tg(2n - a)
Приложения:
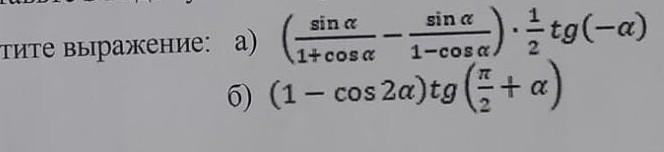
Ответы
Автор ответа:
3
Ответ:
Применяем формулы синуса и косинуса двойного аргумента , формулы приведения , тригонометрическую единицу :
Похожие вопросы
Предмет: Биология,
автор: nyawka18
Предмет: МХК,
автор: sofiiakostiuk
Предмет: Математика,
автор: jejdhhx
Предмет: Физика,
автор: kormakovdaniil24
Предмет: Физика,
автор: kirilmelnikov15