Question

диагональ АС прямоугольника АВСД равна 3 см и составляет со стороной АД угол 37 градусов. найдите площадь прямоугольника АВСД

Answer 1

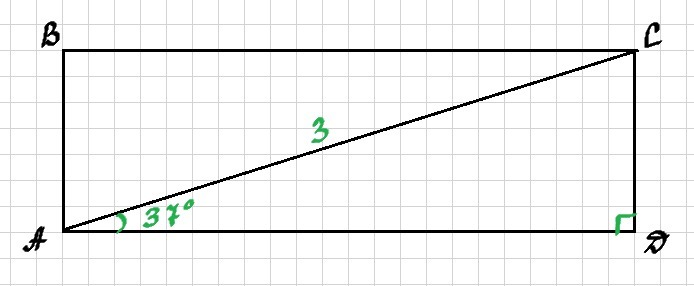
Диагональ делит прямоугольник на два равных прямоугольных треугольника. Рассмотрим ΔАСD (см. прикрепленный рисунок).

АС является гипотенузой в ΔАСD. АС = 3. Также известен острый угол в этом треугольнике ∠CAD = 37°.

Через синус и косинус найдем катеты треугольника АСD.

Синус острого угла в прямоугольном треугольнике - отношение противолежащего катета к гипотенузе.

$sin(A)=frac{CD}{AC}\ \sin37^o=frac{CD}{3}\ \CD=3sin37^o$

Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета к гипотенузе.

$cos(A)=frac{AD}{AC}\ \cos37^o=frac{AD}{3}\ \AD=3cos37^o$

CD и AD являются шириной и длиной в прямоугольника АВСD.

$S_{ABCD}=CD*AD\ \S_{ABCD}=3sin37^o*3cos37^o=9sin37^o*cos37^o=frac{9*2sin37^o*cos37^o}{2}=frac{9*sin(2*37^o)}{2}=frac{9}{2}sin74^o=4,5*sin74^o$

Ответ: $S_{ABCD}=4,5*sin74^o$ см².