Помогите сделать эти 2 задания. Фото приложено. Попрошу с более понятный объяснением

Ответы
Ответ:
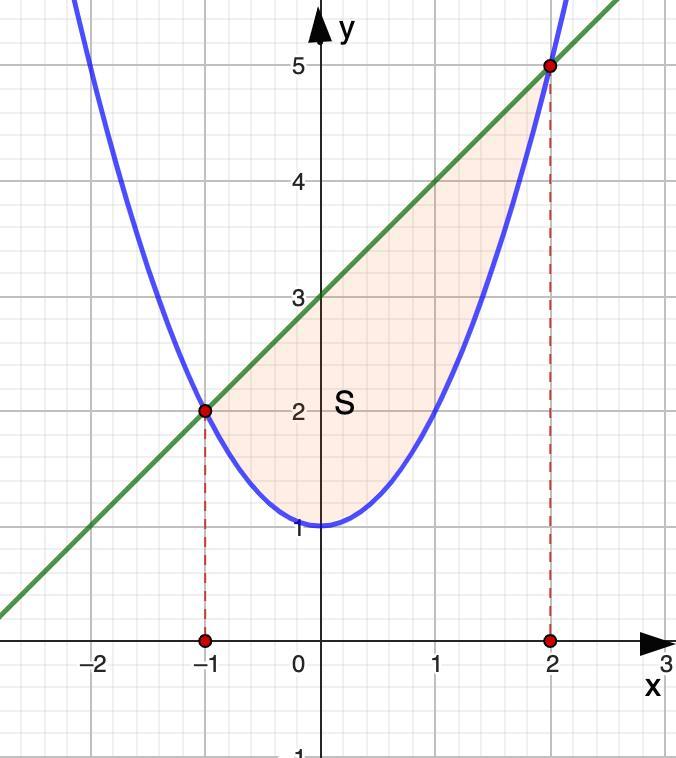
5. Площадь фигуры равна 4,5 ед².
7.
Пошаговое объяснение:
5. Найдите площадь фигуры, ограниченной графиками функций:
у = 1+x² и y = x + 3.
7. используя геометрическое содержание интеграла, вычислите:
5. у = 1 + x² и y = x + 3.
Найдем точки пересечения графиков. Для этого решим систему:
1 + x² = x + 3
x² - x - 2 = 0
По теореме Виета:
х₁ = 2; х₂ = -1
1) у = 1 + х²
- квадратичная функция, график парабола, ветви вверх.
Этот график получается из графика у = х² путем сдвига на одну единицу вверх.
2) у = х + 3
- линейная функция, график прямая.
- Площадь фигуры найдем по формуле:
У нас а = -1; b = 2; f₂(x) = x + 3; f₁(x) = 1 + x²
Площадь фигуры равна 4,5 ед².
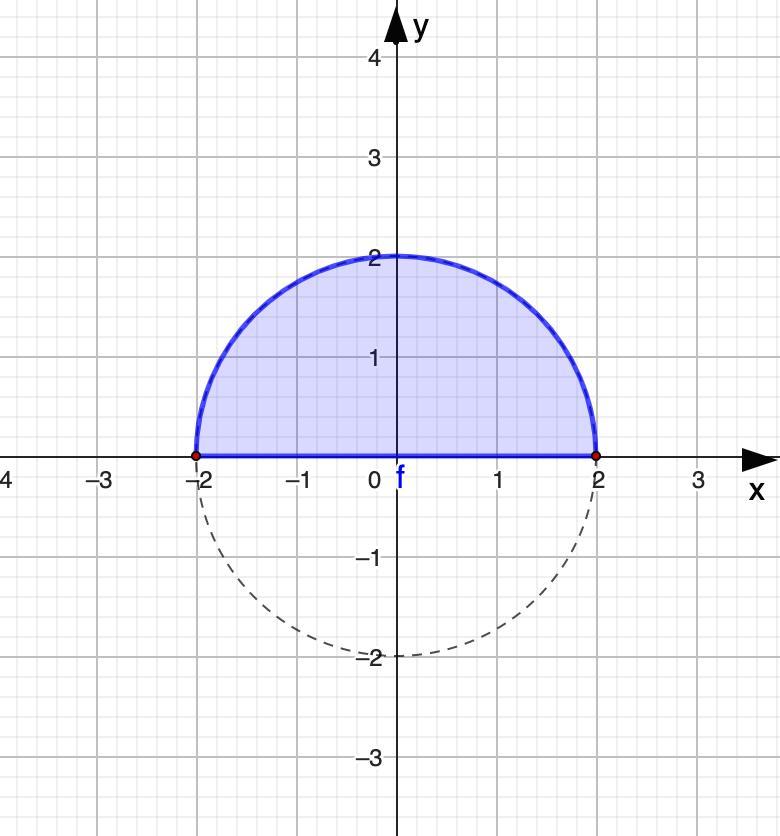
7.
- Геометрический смысл определенного интеграла - площадь криволинейной трапеции, образованной графиком подынтегральной функции, осью Ох и прямыми х = а и х = b.
Преобразуем подинтегральную функцию:
Область определения функции:
4 - х² ≥ 0 ⇒ х² - 4 ≤ 0 ⇒ -2 ≤ х ≤ 2
D(y) = [-2; 2]
Возведем в квадрат обе части:
у² = 4 - х²
у² + х² = 4
- уравнение окружности с центром в начале координат и радиусом 2.
Так как пределы интегрирования от (-2) до 2 и у ≥ 0, то имеем половину круга.
⇒ Значение интеграла:
(ед²)
#SPJ1