Question

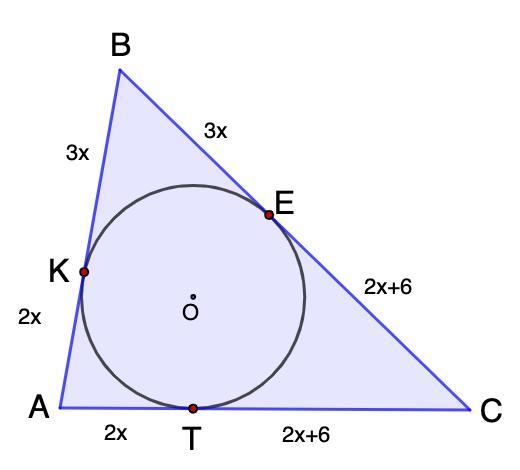
Коло вписане в трикутник ABC і дотикається сторони AB в точці K, сторони BC в точці E, сторони AC в точці T. Відомо що AK:KB=2:3 і CE на 6 см більше за AT. Знайдіть сторони трикутника ABC якщо периметр трикутника ABC дорівнює 146 см

Answer 1

Ответ:

Стороны треугольника равны:

АВ = $\displaystyle AB= 47\frac{6}{7}\;_{CM};\; BC= 53\frac{6}{7}\;_{CM};\;AC=44\frac{2}{7}\;_{(CM)}$

Объяснение:

Круг вписан в треугольник ABC и касается стороны AB в точке K, стороны BC в точке E, стороны AC в точке T. Известно что AK: KB=2: 3 и CE на 6 см больше AT. Найдите стороны треугольника ABC если периметр треугольника ABC равен 146 см.

Дано: ΔАВС;

Окр.О - вписана в ΔАВС;

К, Е и Т - точки касания со сторонами АВ, ВС и АС соответственно.

AK: KB=2: 3; СЕ = АТ + 6 см

Р(АВС) = 146 см.

Найти: АВ, ВС, АС.

Решение:

• Отрезки касательных к окружности, проведенных из одной точки, равны.

AK: KB=2: 3

Пусть АК = 2х см; КВ = 3х см.

⇒ АК = АТ = 2х см; КВ = ВЕ = 3х см; ТС = СЕ = АТ + 6 см = 2х + 6 см.

• Периметр - сумма длин всех сторон треугольника.

Р(АВС) = АВ + ВС + АС

146 = АК + КВ + ВЕ + ЕС + СТ + ТА

146 = 2х + 3х + 3х + 2х + 6 + 2х + 6 + 2х

14х = 146 - 12     |:14

$x = \frac{134}{14}\\ \\\displaystyle x=\frac{67}{7}$

Найдем стороны:

$\displaystyle AB=5x=5\cdot \frac{67}{7}= \frac{335}{7} =47\frac{6}{7}$   (cм)

$\displaystyle BC=5x+6=47\frac{6}{7}+6=53\frac{6}{7}$   (см)

$\displaystyle AC=4x+6=4\cdot\frac{67}{7} +6=38\frac{2}{7}+6=44\frac{2}{7}$   (см)

#SPJ1