Предмет: Алгебра,
автор: darinazabaeva9
помогите, с решением пожалуйста
Приложения:
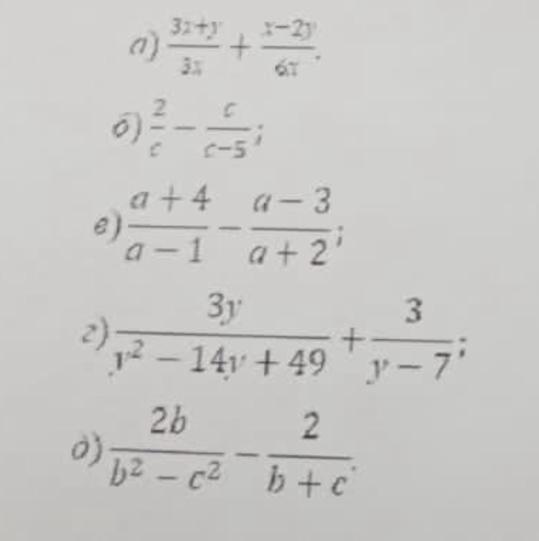
Ответы
Автор ответа:
3
а)
б)
в)
г)
д)
darinazabaeva9:
спасибо большое^^
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Информатика,
автор: Mariga06
Предмет: Қазақ тiлi,
автор: karolinagrishina2012
Предмет: Українська мова,
автор: superziminalena
Предмет: Русский язык,
автор: kalasnikovakarolina2