Question

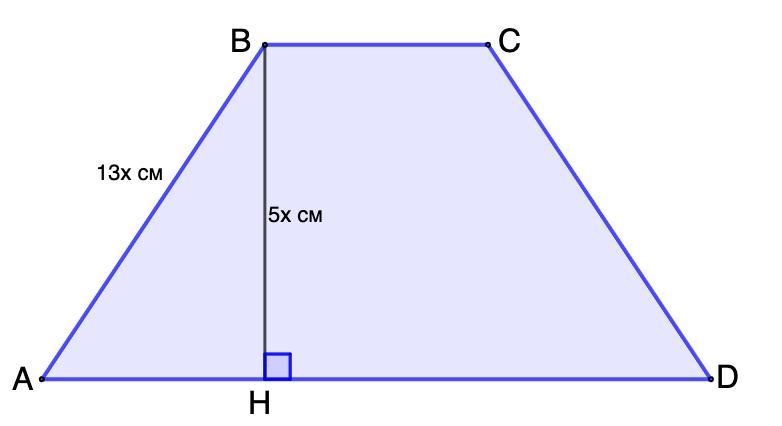
у рівнобічної трапеції, різниця основ дорівнює 48см, а периметр 128см. Обчислити площу трапеції, якщо бічна сторона і висота відносяться, як 13:5​

Answer 1

Ответ:

Площадь трапеции равна 380 см².

Объяснение:

В равносторонней трапеции, разница оснований равна 48 см, а периметр 128 см. Вычислить площадь трапеции, если боковая сторона и высота относятся, как 13 : 5​.

Дано: ABCD - равнобедренная трапеция;

AD - BC = 48 см;

P(ABCD) = 128 см

АВ : ВН = 13 : 5

Найти: S(ABCD)

Решение:

AD - BC = 48 см  

• Высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшая из которых равна полуразности оснований.

⇒ АН = (AD - BC) : 2 = 48 : 2 = 24 (см)

Рассмотрим ΔАВН - прямоугольный.

АВ : ВН = 13 : 5

Пусть ВН = 5х см, тогда АВ = 13х см.

По теореме Пифагора:

АВ² = АН² + ВН²

169х² = 24² + 25х²

144х² = 576     |:144

x² = 4

x = 2

⇒ AB = CD = 26 см; BH = 10 см

P(ABCD) = 128 см

• Периметр - сумма длин всех сторон трапеции.

AD - BC = 48 см    ⇒     AD = BC + 48

P(ABCD) = AB + BC + CD + AD

128 = 26 + BC + 26 + BC + 48

2BC = 28     |:2

BC = 14 см, AD = 14 + 48 = 62 (см)

• Площадь трапеции равна произведению полусуммы оснований на высоту.

$\displaystyle S(ABCD) = \frac{BC+AD}{2}\cdot BH=\frac{14+62}{2}\cdot 10=380$   (см²)

Площадь трапеции равна 380 см².

#SPJ1