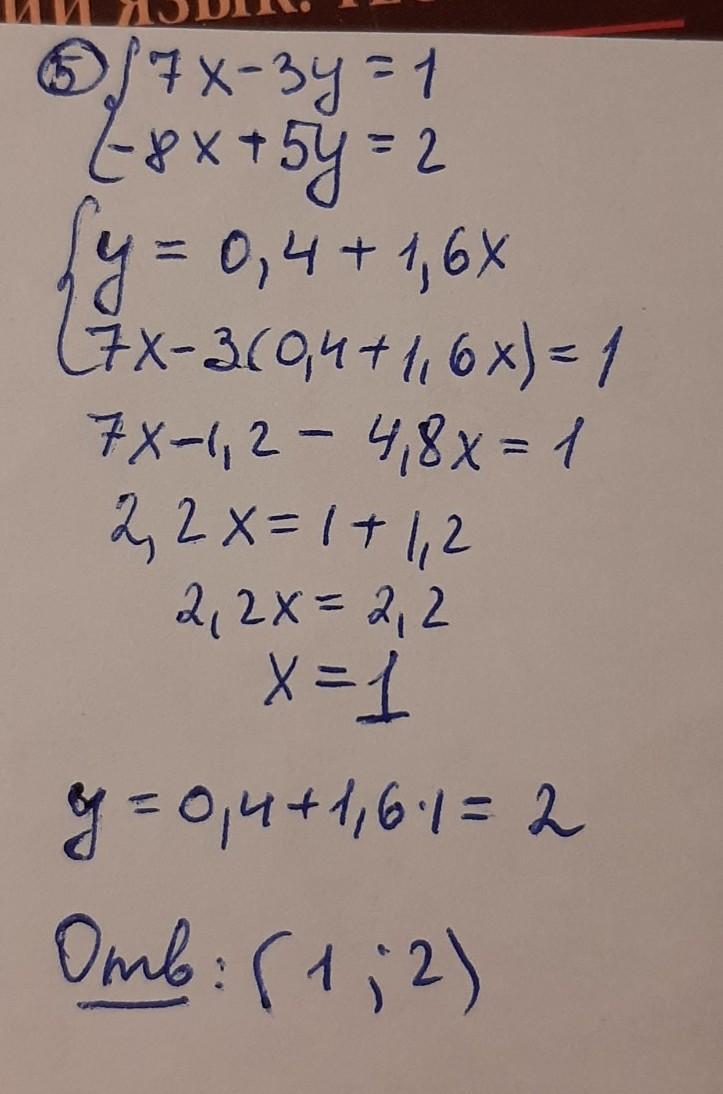1)x=5y+4 4x-3y=-1 2)2x+5y=-7 3x-y=15 3)4x-y=7 2x+y=11 4)6y+10x=8 5x-6y=7 5)7x-3y=1 5y-8x=2
решите систему уравнений методом подстановки
пж помогите даю 58 баллов
Ответы
Ответ:
Для решения системы уравнений методом подстановки нужно сначала выразить одну из переменных через другую в одном из уравнений, а затем подставить это выражение в другое уравнение системы.
Начнем с первого уравнения: x=5y+4. Заменим x во втором уравнении системы на это выражение: 4x-3y=-1 станет 4(5y+4)-3y=-1. Решая это уравнение, получаем y=−2/23. Затем подставляем найденное значение y в первое уравнение системы и находим x: x=5y+4=5(−2/23)+4=13/23. Таким образом, решение системы уравнений: x=13/23, y=−2/23.
Выразим y через x из второго уравнения: 5y=-2x-7. Подставим это выражение в первое уравнение системы: 2x+(-2x-7)=-15, откуда x=2. Затем найдем y, подставив x=2 в любое из уравнений: 3(2)-y=15, y=-9. Таким образом, решение системы уравнений: x=2, y=-9.
Выразим y через x из второго уравнения: y=11-2x. Подставим это выражение в первое уравнение системы: 4x-(11-2x)=7, откуда x=3. Затем найдем y, подставив x=3 в любое из уравнений: 4(3)-y=7, y=5. Таким образом, решение системы уравнений: x=3, y=5.
Выразим y через x из второго уравнения: y=(5x-7)/6. Подставим это выражение в первое уравнение системы: 10x+5((5x-7)/6)=8, откуда x=2. Затем найдем y, подставив x=2 в любое из уравнений: 6y+10(2)=8, y=-1. Таким образом, решение системы уравнений: x=2, y=-1.
Выразим y через x из второго уравнения: y=(8x+2)/5. Подставим это выражение в первое уравнение системы: 7x-3((8x+2)/5)=1, откуда x=−7/23. Затем найдем y, подставив x=−7/23 в любое из уравнений: 5(−7/23)-6y=7, y=−37/46. Таким образом, решение системы уравнений: x=−7/23, y=−37/46
Решение на прикреплённой фотографии