Предмет: Алгебра,
автор: timursaduakasov5
Помогите пожалуйста
Приложения:
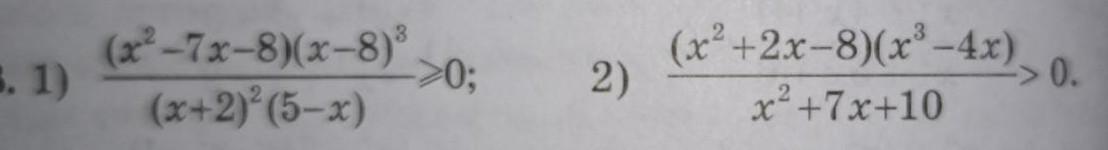
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: seamsniwk
Предмет: Биология,
автор: LunaLavian12
Предмет: Литература,
автор: Аноним
Предмет: Физика,
автор: saadakovj
Предмет: Английский язык,
автор: Sarik2009