помогите решить пожалуйста
Ответы
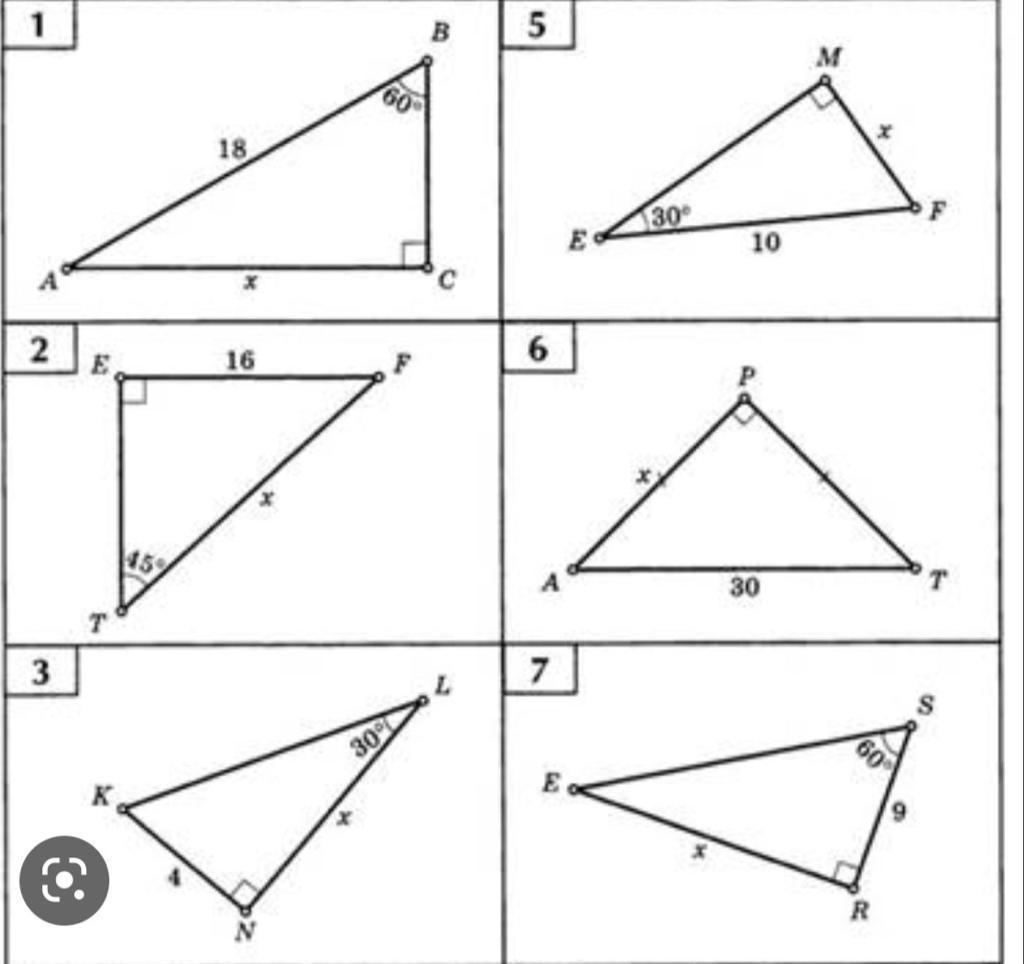
Используем теорему, согласно которой в треугольнике с углами 90, 60 и 30°, гипотенуза будет больше меньшего катета в 2 раза, а второй катет будет больше меньшего в √3 раза. Также, если треугольник равнобедренный и его углы равны 45°, то катеты будут равны, гипотенуза же будет дольше них в √2 раза.
1. AB = 18 - гипотенуза,
BC - меньший катет,
AC = x - больший катет.
Для начала найдем меньший катет BC:
BC = AB/2 = 18/2 = 9
Следовательно, можно найти и х (AC):
AC = BC√3 = 9√3
2. Находим здесь гипотенузу равнобедренного треугольника:
EF = ET = 16 (так как углы 45°),
FT = x - гипотенуза.
FT = EF√2 = 16√2
3. В этом пункте нам не дана гипотенуза, но мы должны найти больший катет:
KL - гипотенуза,
LN = x - больший катет,
NK = 4 - меньший катет.
Согласно теореме, больший катет больше меньшего в √3 раза:
LN = NK√3 = 4√3
5. Здесь то же самое, но надо найти меньший катет:
EF = 10 - гипотенуза,
EM - больший катет,
MF = x - меньший катет.
Находим меньший катет, согласно теореме:
MF = EF/2 = 10/2 = 5
6. Здесь представлен равнобедренный треугольник:
AT = 30 - гипотенуза,
AP = PT = x (так как, равнобедренный тр.),
Совершаем действия как в пункте 2), только наоборот:
AP = AT/√2 = 30/√2 = 15√2
7. SR = 9 - меньший катет,
RE = x - больший катет,
ES - гипотенуза.
Решение:
RE = SR√3 = 9√3