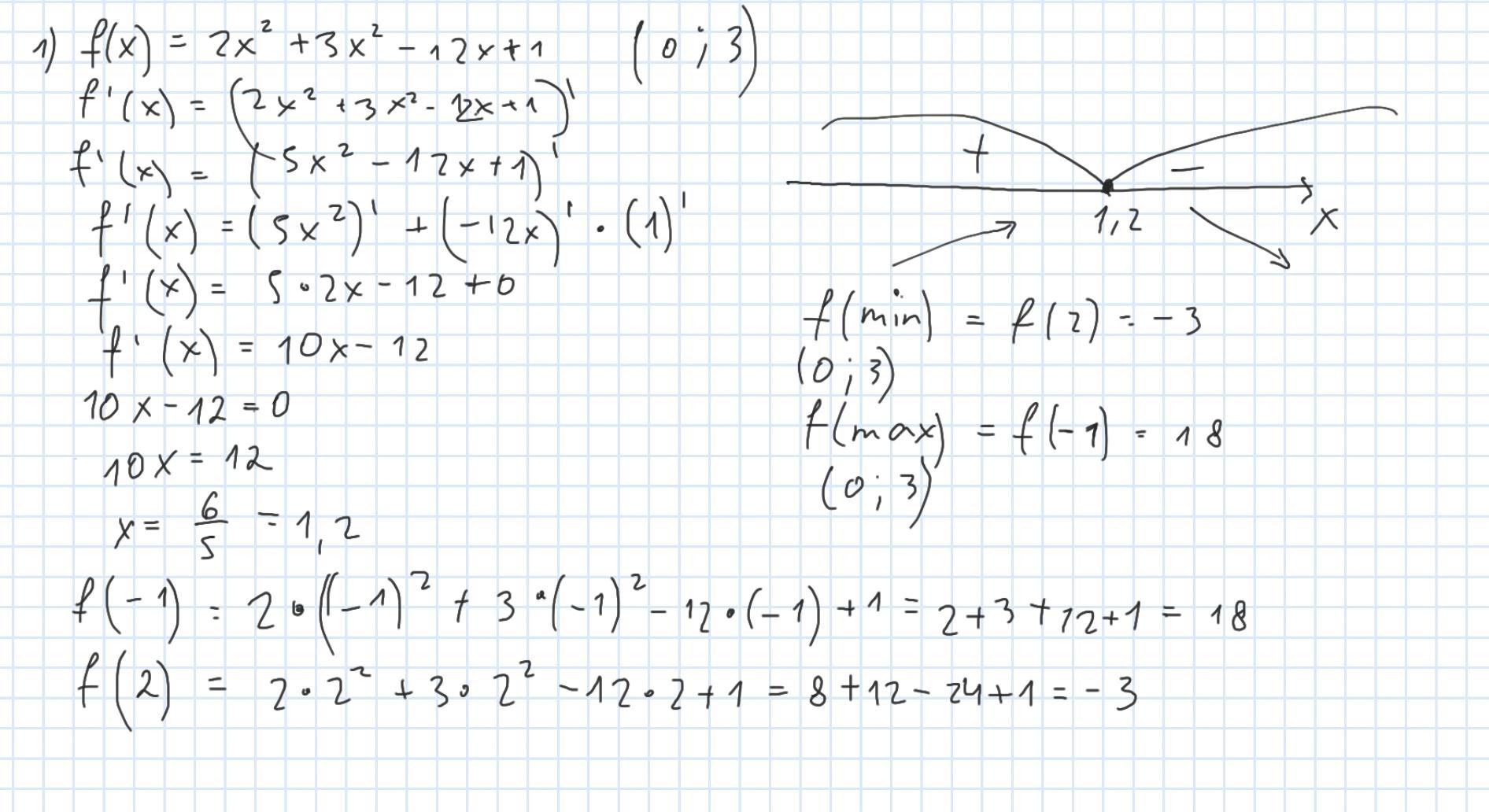Знайдіть найбільше та найменше значення функції на вiдрiзку
Найдите наибольшие и наименьшие значение функции на отрезке
1)f(x)=2x²+3x²-12x+1 (0;3)
2)f(x)=x³-2x|x-2| (0;3)
Помогите пожалуйста!
Ответы
f'(x) = 4x - 12
Знаходимо критичні точки, при яких f'(x) = 0:
4x - 12 = 0
x = 3
Також перевіримо значення функції в кінцях відрізка:
f(0) = 1
f(3) = 28
Отже, найменше значення функції на відрізку [0, 3] дорівнює 1, а найбільше - 28.
Для того, щоб знайти найбільше та найменше значення функції f(x) на відрізку [0, 3], спочатку розіб'ємо відрізок [0, 3] на дві частини: [0, 2] та [2, 3]. Далі знайдемо функцію f(x) на кожній з цих частин.
На відрізку [0, 2], знак модуля |x-2| дорівнює від'ємному значенню, тому:
f(x) = x³ - 2x*(-x+2) = x³ + 2x² - 4x
f'(x) = 3x² + 4x - 4
Знаходимо критичні точки, при яких f'(x) = 0:
3x² + 4x - 4 = 0
x = (-2 ± √10) / 3
Також перевіримо значення функції в кінцях відрізка:
f(0) = 0
f(2) = -8
Отже, на відрізку [0, 2] найменше значення функції дорівнює -8, а найбільше може бути досягнуте у одній з критичних точок, які знаходяться за межами відрізка.
На відрізку [2, 3], знак модуля |x-2| дорівнює додатньому значенню, тому:
f(x) = x³ - 2x*(x-2) = -x³ + 4x² - 4x
f'(x) = -3x² + 8x - 4
Знаходимо критичні точки, при яких f'(x) = 0:
-3x² + 8x - 4 = 0x
Ответ:
дай лучший ответ пж
Пошаговое объяснение: