Предмет: Математика,
автор: Skeetusrt
Знайти похідну функції.
Приложения:
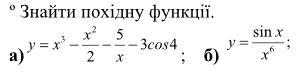
Ответы
Автор ответа:
2
а)
б)
Похожие вопросы
Предмет: Українська література,
автор: sasha7256sasha
Предмет: Химия,
автор: Ergibovalim
Предмет: Геометрия,
автор: sf2807918
Предмет: Русский язык,
автор: trifonovad2007
Предмет: Математика,
автор: olganisirikova