Предмет: Алгебра,
автор: urinbasarovadiana7
2sin2x*tgx+2cos^2x
ДАЮ 20 БАЛЛОВ ПОЖАЛУЙСТА РЕШИТЕ СЕЙЧАС
Ответы
Автор ответа:
2
Ответ:
Упростить выражение .
Применяем формулу синуса двойного угла , основное тригонометрическое тождество .
Приложения:
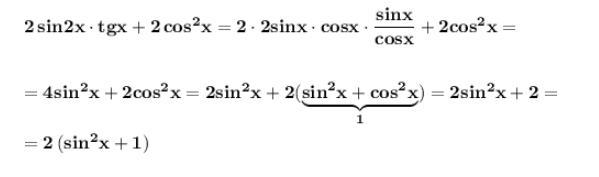
urinbasarovadiana7:
Спасиьо ваи огромное!!!!!!
а как 4sin²x превратился в 2sin²x
4sin²x = 2sin²x + 2sin²x
Похожие вопросы
Предмет: Физика,
автор: userqwek2009
Предмет: Химия,
автор: duck480
Предмет: Українська література,
автор: Аноним
Предмет: Алгебра,
автор: adylzunusov2
Предмет: Алгебра,
автор: Bzhenchishchikovich