Question

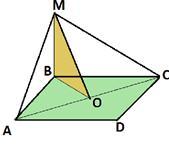
АВСD квадрат, АВ = 2 см, ВМ = 4 см, ВМ ⊥(АВС). Знайдіть МА

Answer 1

Ответ:

З властивостей прямокутного трикутника ВМС можна знайти довжину ВС за теоремою Піфагора:

ВС² = ВМ² + СМ² = 4² + (АВ - АМ)²

Так як АМ = АВ - ВМ, то ВС² = 4² + (2 - 4)² = 16 + 4 = 20

Отже, ВС = √20 = 2√5

Застосовуючи теорему Піфагора до трикутника АВС, маємо:

АС² = АВ² + ВС² = 2² + (2√5)² = 4 + 20 = 24

Таким чином, АС = √24 = 2√6

Застосовуючи теорему Піфагора до трикутника АМС, маємо:

АМ² + СМ² = АС²

АМ² + (2 - ВМ)² = (2√6)²

АМ² + (2 - 4)² = 24

АМ² = 24 - 4 = 20

Отже, АМ = √20 = 2√5

Відповідь: МА = 2√5 см.