Предмет: Геометрия,
автор: nursultanisken14
С дано и оформлением задача Правильный шестиугольник вписан в окружность. Его периметр равен 24√3 см. Найдите сторону правильного треугольника вписанного в эту же окружность.
Ответы
Автор ответа:
1
Ответ: Сторона правильного треугольника вписанного в эту же окружность равна 24 см
Объяснение:
a₃ - длина стороны треугольника вписанного в окружность
a₆ - длина стороны шестиугольника вписанного в окружность
Дано :
a₆ = 24√3 см
a₃ = ? см
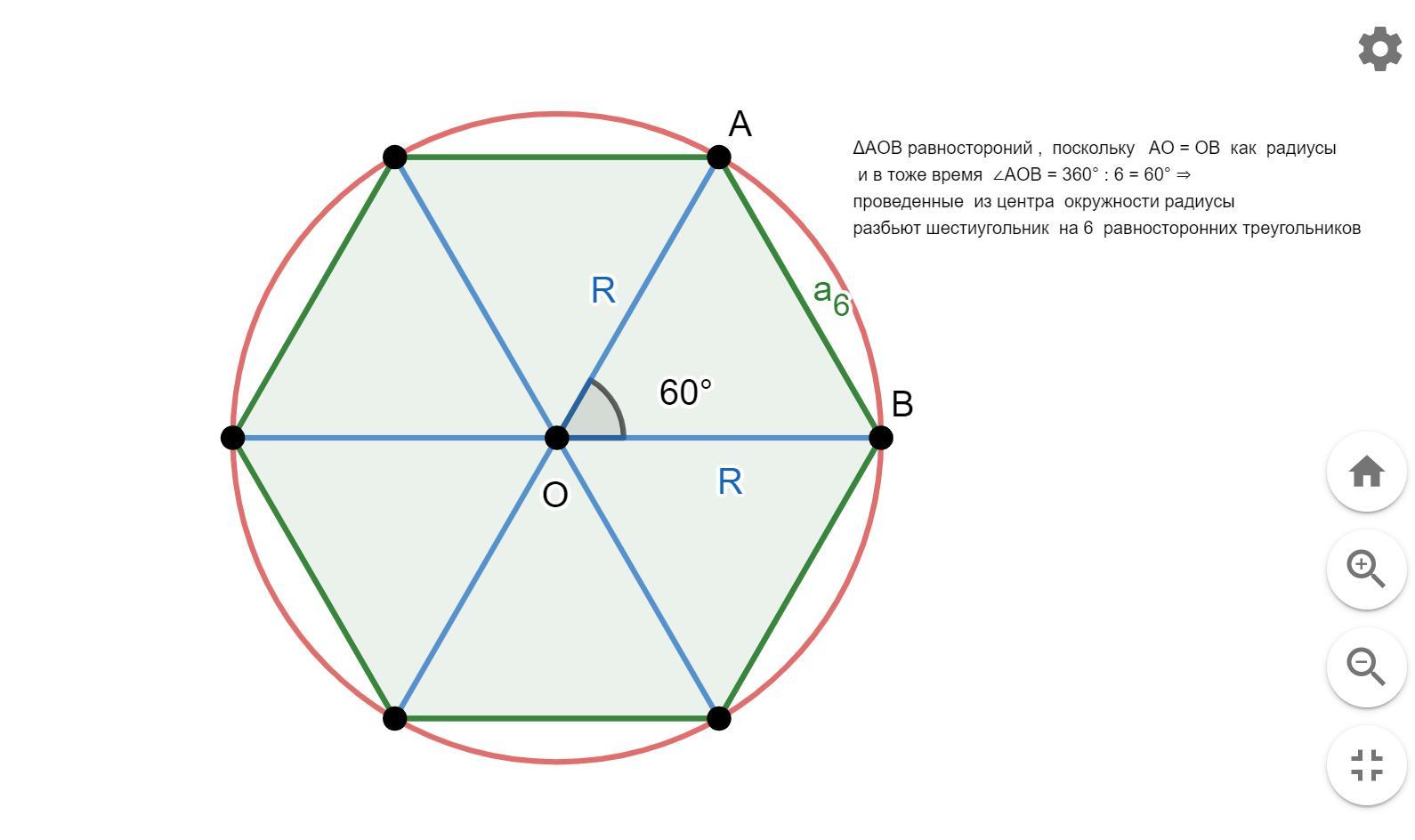
Нарисовав шестиугольником который вписан в окружность , проводим из центра окружности радиусы к вершинам данного шестиугольника , теперь легко видеть , что мы разбили наш шестиугольник на 6 равносторонних треугольников , соответственно
R = AB = a₆ = 24√3
А взаимосвязь между радиусом описанной окружности вокруг равностороннего Δ-ка и его стороной раскрывается формулой :
(см)
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: tracukv882
Предмет: Французский язык,
автор: meri1774
Предмет: История,
автор: nekoglaafan23
Предмет: Русский язык,
автор: Аноним
Предмет: Биология,
автор: Katy0076