В равнобедренный треугольник вписана окружность, которая точкой касания делит боковую сторону треугольника в отношении 7:4, считая от вершины. Найдите стороны треугольника, если периметр равен 270.
ПОЖАЛУЙСТА С ЧЕРТЕЖОМ И ПОДРОБНО

Ответы
Ответ:
Боковые стороны равнобедренного треугольника равны 99 ед.
Основание равнобедренного треугольника равно 72 ед.
Объяснение:
В равнобедренный треугольник вписана окружность, которая точкой касания делит боковую сторону треугольника в отношении 7:4, считая от вершины. Найдите стороны треугольника, если периметр равен 270.
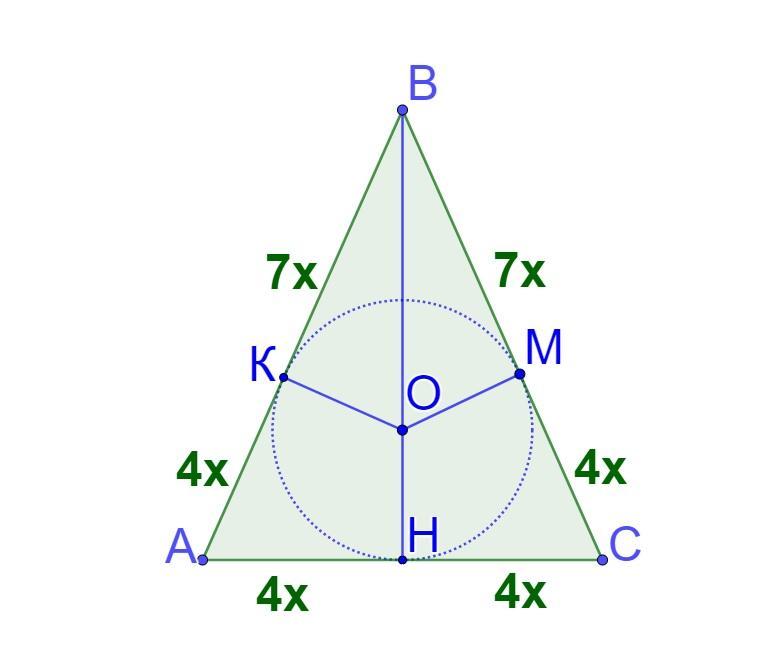
Дано: ΔАВС - равнобедренный, АВ=ВС, ВК:АК=7:4, Р(ΔАВС)=270, т.О - центр вписанной окружности. ОК⊥АВ, ОМ⊥ВС, ОН⊥АС - как радиусы вписанной окружности.
Найти: АВ, ВС, АС.
РЕШЕНИЕ:
Точки касания с окружностью - К,М,Н.
Пусть ВК=7х, АК=4х, где х - коэффициент пропорциональности.
АВ=ВС=ВК+АК=7х+4х=11х
Так как отрезки касательных, проведенных из одной точки равны, то:
АН=АК=4х,
НС=АН=4х - так как ВН - высота, которая в равнобедренном треугольнике является также медианой.
АС=АН+НС=4х+4х=8х
Периметр треугольника равен сумме всех его сторон:
Р(ΔАВС)=АВ+ВС+АС
Составим и решим уравнение:
11х+11х+8х=270
30х=270
х=9
Таким образом:
АВ=ВС=11·9=99 (ед)
АС=8·9=72 (ед)
Ответ: 99 ед, 99 ед, 72 ед
#SPJ1