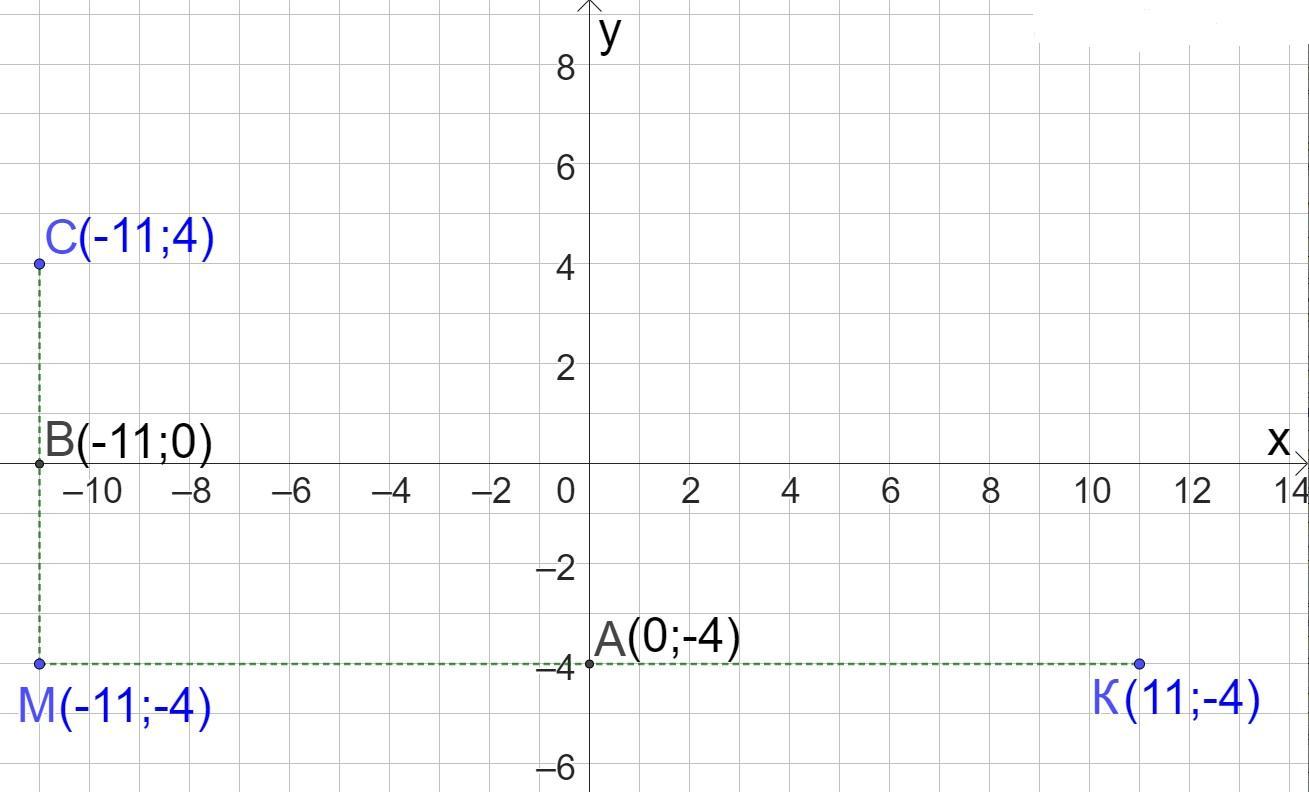
Дано точку К(11; -4). Точка М симетрична точці К відносно осі ординат. Знайдіть координати точки С, яка симетрична точці М відносно осі абсцис.
Ответы
Ответ:
С(-11;4)
Объяснение:
Дано точку К(11; -4). Точка М симетрична точці К відносно осі ординат. Знайдіть координати точки С, яка симетрична точці М відносно осі абсцис.
- Дві точки X та X' називають симетричними відносно прямої l, якщо пряма l є серединним перпендикуляром до відрізка XX'.
1.
Маємо точку К(11;-4) і пряму, яка є віссю Oу. За означенням вісь Oу – серединний перпендикуляр до відрізка МК, тому відрізок МК перпендикулярний до осі ординат МК⊥Oу і паралельний до осі абсцис МК||Oх. Це означає, що точка А(0;-4) – середина відрізка МК, а точка М має координати (-11;-4).
Отже, якщо точки, симетричні відносно осі ординат Oу, то вони мають протилежні абсциси та однакові ординати.
М(-11;-4)
2.
Маємо точку М(-11;-4) і пряму, яка є віссю Ox. За означенням вісь Ox – серединний перпендикуляр до відрізка МС, тому відрізок МС перпендикулярний до осі абсцис МС⊥Ox і паралельний до осі ординат МС||Oy. Це означає, що точка В(-11;0) – середина відрізка МС, а точка С має координати (-11;4).
Отже, якщо точки, симетричні відносно осі абсцис Ox, то вони мають однакові абсциси та протилежні ординати.
С(-11;4)
Відповідь: С(-11;4)
#SPJ1