Предмет: Геометрия,
автор: dormmys
На рисунку SC=SB, SB=AB, SD=AD. Знайдіть кут SCB, якщо кут
DBA=64 градуса.
Приложения:

Ответы
Автор ответа:
3
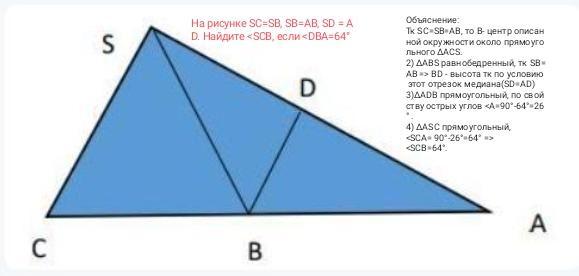
На рисунке SC=SB, SB=AB, SD = AD. Найдите <SCB, если <DBA=64°
Объяснение:
Тк SC=SB=AВ, то В- центр описанной окружности около прямоугольного ∆АСS.
2) ∆АВS равнобедренный, тк SB=AB => BD - высота тк по условию этот отрезок медиана(SD=AD)
3)∆ADВ прямоугольный, по свойству острых углов <А=90°-64°=26° .
4) ∆АSC прямоугольный,
<SСА= 90°-26°=64° =>
<SСВ=64°.
Приложения:
Автор ответа:
1
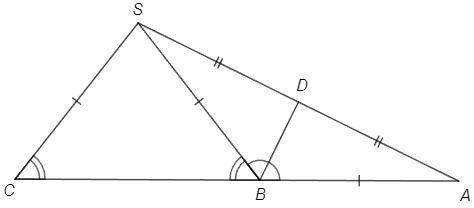
В равнобедренном треугольнике биссектриса/медиана/высота к основанию совпадают.
△SBA -р/б (SB=AB) => BD - медиана и биссектриса
Биссектриса делит угол пополам.
∠SBA =2∠DBA =64°·2 =128°
∠SBC =180°-∠SBA =180°-128° =52°
В равнобедренном треугольнике углы при основании равны.
△CSB -р/б (SC=SB) => ∠SCB=∠SBC=52°
Приложения:
Похожие вопросы
Предмет: Биология,
автор: j04819607
Предмет: Литература,
автор: g977190
Предмет: География,
автор: tiktoker228biglox
Предмет: Алгебра,
автор: Irunaaaa