дан правильный треугольник высота которого равна 12 см найдите радиус описанной окружности и площадь треугольника
Ответы
Відповідь:
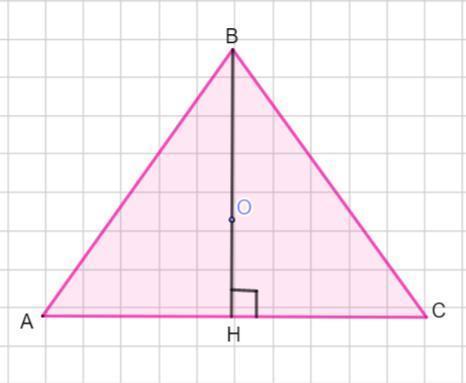
Радиус окружности описанной около треугольника равен 8 смБ) 8 см.Пошаговое объяснение:По условию задан Δ АВС -правильный. Высота ВН = 12см.Найдем радиус окружности, описанной около Δ АВС .Пусть точка О - центр окружности, описанной около треугольника.Если треугольник правильный, то это центр треугольника, то есть точка пересечения медиан, биссектрис и высот треугольника.Если точка О - точка пересечения медиан, то медианы в треугольнике пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины.По условию ВН = 12 см . В правильном треугольнике высота ВН является медианой.Точка О делит медиану ВН на два отрезка ВО и ОН , длина отрезка ВО в 2 раза больше, чем длина отрезка ОН. Значит, cм.Отрезок ВО является радиусом описанной окружности.R=8 сми тогда ответ Б) 8 см .
Відповідь:
Ответ: радиус описанной окружности равен 8 см, площадь треугольника равна 12√3 см².
Пояснення:
Радиус описанной окружности правильного треугольника равен половине длины его стороны. Пусть сторона треугольника равна a. Тогда высота h, проведенная к этой стороне, будет являться биссектрисой и медианой этой стороны, и мы можем использовать теорему Пифагора для нахождения длины стороны и радиуса:
�
2
=
(
2
3
ℎ
)
2
+
�
2
a
2
=(
3
2
h)
2
+r
2
�
2
=
4
9
ℎ
2
+
�
2
a
2
=
9
4
h
2
+r
2
Так как треугольник правильный, то $a = 2h/\sqrt{3}$ и $h = 12$ см. Подставим эти значения и решим уравнение:
(
2
3
⋅
12
)
2
=
4
9
⋅
1
2
2
+
�
2
(
3
2
⋅12)
2
=
9
4
⋅12
2
+r
2
�
2
=
(
2
3
⋅
12
)
2
−
4
9
⋅
1
2
2
r
2
=(
3
2
⋅12)
2
−
9
4
⋅12
2
�
2
=
64
r
2
=64
�
=
8
см
r=8 см
Теперь можно найти площадь треугольника, используя формулу:
�
=
3
4
�
2
S=
4
3
a
2
�
=
3
4
(
2
3
⋅
12
)
2
S=
4
3
(
3
2
⋅12)
2
�
=
3
4
⋅
144
3
S=
4
3
⋅
3
144
�
=
3
4
⋅
48
S=
4
3
⋅48
�
=
12
3
см
2
S=12
3
см
2