Предмет: Алгебра,
автор: mollibarbi7
Знайдіть похідну функції у=х3-2cosx+3
Приложения:
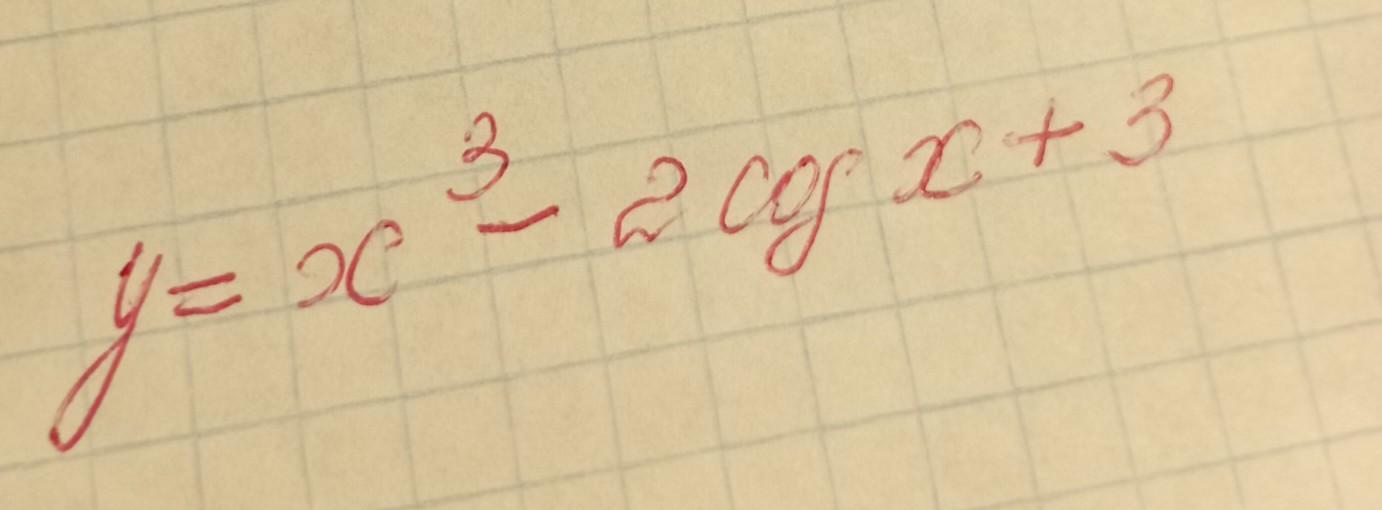
Ответы
Автор ответа:
0
Щоб знайти похідну функції у=х³-2cos(x)+3, потрібно взяти похідну кожного з її компонентів та застосувати правила диференціювання.
Для диференціювання функції y = х³ ми використовуємо правило диференціювання мономів: якщо y = xⁿ, то y' = nx^(n-1).
Отже, застосовуючи це правило, ми отримуємо:
y' = 3x² - 2(-sin(x)) + 0
Згідно правила диференціювання тригонометричних функцій, похідна від cos(x) дорівнює -sin(x).
Отже, похідна функції у=х³-2cos(x)+3 дорівнює:
y' = 3x² + 2sin(x)
О:))
Похожие вопросы
Предмет: Українська мова,
автор: viksk
Предмет: Математика,
автор: zharskae
Предмет: Химия,
автор: makarenkotanya777
Предмет: Физика,
автор: dhshshco
Предмет: Математика,
автор: Cuce4ka228