розв'яжіть рівняння. (2x+1)^2/25 - x-1/3 =x СРОЧНО!!!!!
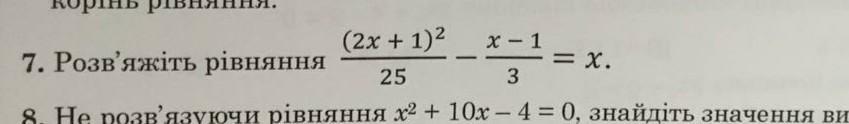
Ответы
Ответ
Для розв'язання цього рівняння, спочатку приведемо всі дроби до спільного знаменника, щоб уникнути роботи з дробовими числами. У цьому випадку спільним знаменником може бути 75, який є множником знаменника 25 у першому доданку та множником знаменника 3 у другому доданку:
(2x + 1)^2/25 - (x - 1)/3 = x
Множимо обидві частини рівняння на 75, щоб усунути дроби:
75 * ((2x + 1)^2/25) - 75 * ((x - 1)/3) = 75 * x
Отримаємо:
3(2x + 1)^2 - 25(x - 1) = 75x
Проведемо операції з розкриттям дужок, множенням, та додаванням, щоб отримати квадратне рівняння:
12x^2 + 12x + 3 - 25x + 25 = 75x
12x^2 - 13x + 28 = 75x
12x^2 - 88x + 28 = 0
Далі можна вирішити це квадратне рівняння, наприклад, за допомогою квадратного кореня, факторизації, або за допомогою квадратного рівняння формули:
x = (-b ± √(b^2 - 4ac)) / (2a),
де a = 12, b = -88, c = 28.
Продовжуючи розв'язування, отримаємо:
x = (88 ± √(88^2 - 4 * 12 * 28)) / (2 * 12)
x = (88 ± √(7744 - 1344)) / 24
x = (88 ± √6400) / 24
x = (88 ± 80) / 24
Таким чином, отримуємо два розв'язки:
x1 = (88 + 80) / 24 = 168 / 24 = 7
x2 = (88 - 80) / 24 = 8 / 24 = 1/3
Отже, рівняння має два розв'язки: x = 7 та x = 1/3.
Объяснение: