Question

Помогите пж
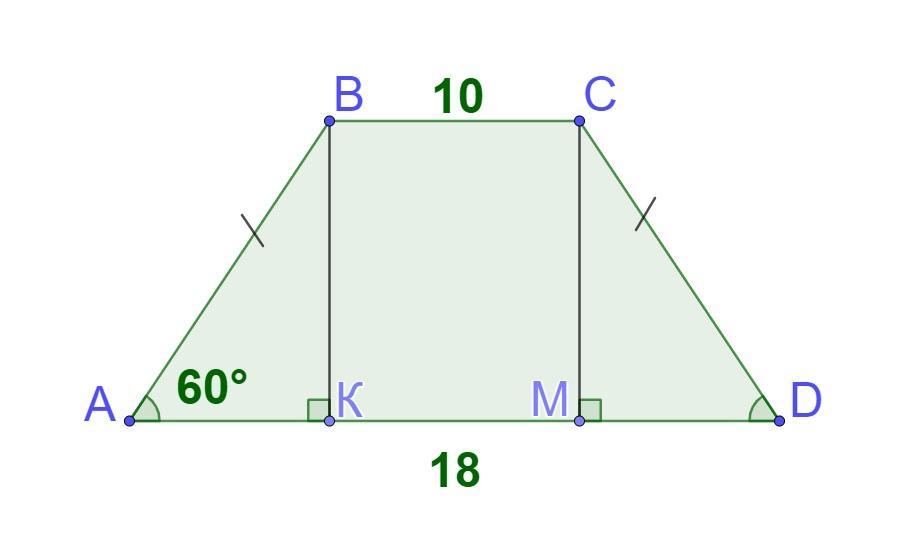
ABCD-рівнобічна трапеція, більша основа 18 см, менша основа 10 см, кут при більшій основі 60 градусів, знайти периметр трапеції

Answer 1

Ответ:

44

Объяснение:

Сначала находим ребро : с= a/cosB

c=4/1/2=8

P=a+b+c+d=10+18+8+8=44

Ответ 44см

Answer 2

Ответ:

Периметр трапеції дорівнює 44 см

Объяснение:

ABCD-рівнобічна трапеція, більша основа 18 см, менша основа 10 см, кут при більшій основі 60 градусів, знайти периметр трапеції.

Нехай дано трапецію ABCD, BC║AD, АВ=СD,ВС=10 см, АD=18 см,

∠А=∠D=60°.

Знайдемо периметр ABCD.

1) Проведемо висоти ВК і СМ. ВК⊥АD, СМ⊥АD.

Розглянемо ΔАВК і ΔDСМ.

• ∠АКВ=∠DМС=90°
• ВК=СМ (висоти)
• АВ=СD (трапеція рівнобока)

Отже, ΔАВК = ΔDСМ (за катетом і гіпотенузою), з цього випливає, що АК=МD.

2) Оскільки BСМK - прямокутник, то KМ=BС=10 (см)

3) АК=МD=(АD-ВС):2=(18-10):2=4 (см)

4) В прямокутному ΔАВК за теоремою про суму кутів прямокутного трикутника знайдемо ∠АВК:

∠АВК=90°-∠А=90°-60°=30°

5) Катет АК=4 см лежить напроти кута АВК=30°, тому (за властивістю) він дорівнює половині гіпотенизи АВ, отже:

АВ=2·АК=2·4=8 (см)

СD=АВ=8 (см)

6) Периметр трапеції дорівнює сумі всіх ії сторін:

Р(ABCD)=АВ+ВС+СD+АD=8+10+8+18=44 (см)

Відповідь: 44 см