Question

30 БАЛЛОВ!!!!!!!
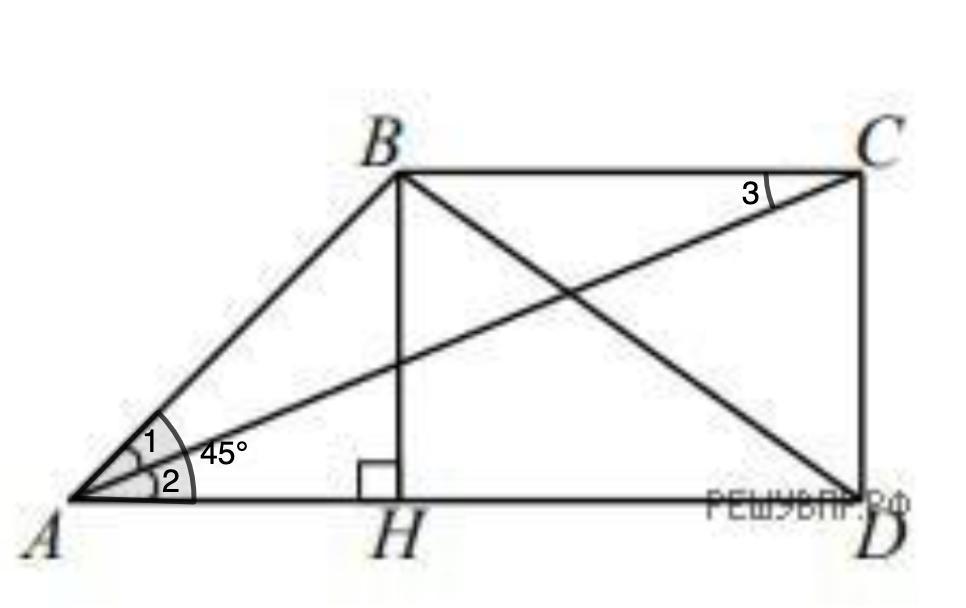
В пря­мо­уголь­ной тра­пе­ции ABCD с ос­но­ва­ни­я­ми AD и BC диа­го­наль АС яв­ля­ет­ся бис­сек­три­сой угла А, рав­но­го 45°. Най­ди­те длину диа­го­на­ли BD, если мень­шее ос­но­ва­ние тра­пе­ции равно 4√2. За­пи­ши­те ре­ше­ние и ответ.​

Answer 1

Ответ:

Длина диагонали BD трапеции равна 4√3 ед.

Объяснение:

В пря­мо­уголь­ной тра­пе­ции ABCD с ос­но­ва­ни­я­ми AD и BC диа­го­наль АС яв­ля­ет­ся бис­сек­три­сой угла А, рав­но­го 45°. Най­ди­те длину диа­го­на­ли BD, если мень­шее ос­но­ва­ние тра­пе­ции равно 4√2.

Дано: ABCD - прямоугольная трапеция:

АС - биссектриса ∠А; ∠А = 45°;

ВС = 4√2.

Найти: BD.

Решение:

Для удобства обозначим углы цифрами.

1. Рассмотрим ΔАВС.

АС - биссектриса

⇒ ∠1 = ∠2

  ∠3 = ∠2 (накрест лежащие при BC || AD и секущей АС)

⇒ ∠1 = ∠3

• Если в треугольнике два угла равны, то он равнобедренный.

⇒ АВ = ВС = 4√2

2. Рассмотрим ΔАВН - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АВН = 90° - ∠А = 90° - 45° = 45°

∠А = ∠АВН   ⇒ ΔАВН - равнобедренный.

Пусть АН = НВ = х

Тогда по теореме Пифагора:

АВ² = АН² + НВ²

32 = 2х²     |:2

х² = 16

x = 4

AH = HB = 4

3. Рассмотрим ΔНВD - прямоугольный.

ВН ⊥AD; CD ⊥ AD; ВС || AD (условие)

⇒ HBCD -  прямоугольник.

⇒ ВС = HD = 4√2

По теореме Пифагора:

BD² = HB² + HD²

BD² = 16 + 32 = 48   ⇒   BD = √48 = 4√3

#SPJ1